Wyznacz równania stycznych do okręgu Marcin: Wyznacz równania wszystkich wspólnych stycznych do paraboli o równaniu y= 1/2x² i okręgu o równaniu x² + ( y + 5/2)² = 2

Basia: było kilka dni temu; identyczne albo bardzo podobne; poszukaj

Tk mysl: Prosta jest styczna do okregu gdy odleglosc od srodka okregu jest rowna promieniowi. Stad odleglosc od punktu (0,−5/2) wynosi √2 Skorzystaj ze wzoru na odleglosc punktu od prostej,przy czym wpierw Wiemy ze prosta jest styczna do paraboli zatem nazwijmy te prosta styczna : y_s = ax + b Skoro styczna do paraboli to spełnia jej rownanie. Co dalej? Hmm

Mila:

	1
f(x)=		x2
	2

	5
x2+(y+		)2=2
	2

	5
S=(0,−		), r=√2
	2

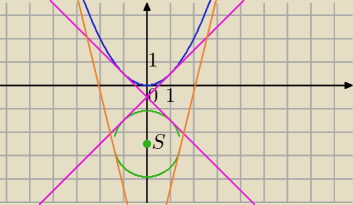
	1
P=(a,		a2) − punkt styczności z parabolą
	2

	1
f'(x)=		*2x=x
	2

f'(a)=a Styczna do paraboli w punkcie P:

	1
y=a*(x−a)+		a2⇔
	2

	1
y=ax−a2+		a2
	2

	1
y=ax−		a2 , styczna ma być wspólna z okręgiem⇔
	2

odległość S od tej prostej jest równa promieniowi s: ax−y−0.5a²=0 równanie ogólne prostej stycznej d(S, s)=U{|a*0+2.5−0.5a²|}{√a²+1=√2⇔ |2.5−0.5a²|=√2*√a²+1 /² (2.5−0.5a²)²=2a²+2 6.25−2.5a²+0.25a⁴=2a²+2 a⁴−18a²+17=0, Δ=256

	18−16
a2=		lub a2=17
	2

a=1 lub a=−1 lub a=√17 lub a=−√17 podstawiaj do wzoru:

	1
s: y=ax−		a2
	2

	1
s1: y=x−
	2

	1
s2: y=−x−
	2

	17
s3: y=√17x−
	2

	17
s4: y=√7x−
	2

=================== posprawdzaj rachunki