Rachunek prawdopodobieństwa - losowy punk ze zbioru michal: Ze zbioru D = {(x,y) ∊ R² : 0 ≤ x ≤ 1 ∧ 2 ≤ y ≤ 4} wybieramy losowo punkt (x,y). W zależności od wartości parametru a ∊ R obliczyć P(y ≤ x + a). Będę bardzo wdzięczny za pomoc w rozwiązaniu lub ewentualne wskazówki.

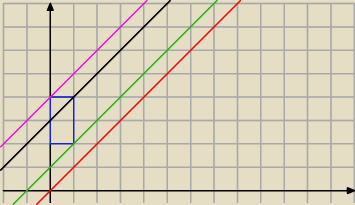
Basia: niebieskie to zadany prostokąt czerwone to prosta y=x (czyli a=0) przesuwamy tę prostą tak żeby był jakiś obszar wspólny prostokąta i półpłaszczyzny pod prostą bo y≤x+a dla a=1 (zielone) to jeden punkt wspólny dla a=4 (fiolet) to już cały prostokąt i dla każdego a≥4 to już będzie cały prostokąt rozrysuj to sobie na oddzielnych rysunkach bo to już się robi nieczytelna dla a∊(1,2> dla a∊(2,3> dla a∊(3;4) bo dla a≤1 P(a)=0 a dla a≥4 P(a) = 2 jeżeli sobie nie poradzisz napisz rozrysujemy to kolejno w tych przedzialach i zastanowimy się co trzeba zrobić bo to będą różne rzeczy

michal: Dziękuję za odpowiedź. Czyli, aby obliczyć P(y ≤ x + a) muszę obliczyć: 1) dla a∊(1,2> pole trójkąta utworzonego pod prostą a =2 2) dla a∊(2,3> pole trapezu pod prostą a =3 3) dla a∊(3;4) pole całego prostokąta. Oczywiście, jest to prawdopodobieństwo, więc każdą obliczoną częśc dzielę przez pole prostokąta, czyli 2?

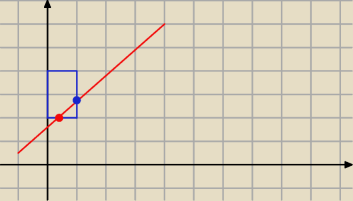
Basia: nie; to jest prosta y=x+a dla a∊(1,2> ona przetnie prawy dłuższy bok prostokąta dostaniesz trójkąt prostokątny; y=2 y=x+a x+a=2 x=2−a x=1 y=x+a y=1+a A(2−a; 2) B(1;a+1) podstawa = 1−(2−a)=a−1 wysokość = a+1−2 = a−1

	(a−1)2
P=
	2

Basia: boki prostokąta zawierają się w prostych o równaniach y=2 (podstawa dolna) y=4 (podstawa górna) x=0 (lewy bok) x=1 (prawy bok)

michal: A no tak, teraz rozumiem! Czyli, dla a∊(2,3> będzie to pole trapezu liczone w ten sposób: 1/2(a−2+a−1) * 1

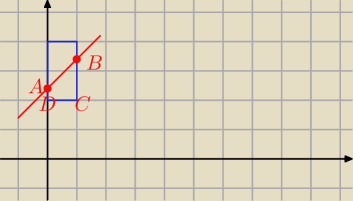
Basia: a∊(2,3> trapez C(1;2) D(0;2) trzeba znaleźć współrzędne A i B A x=0 y=x+a y=0+a=a A(0,a) B x=1 y=x+a y=a+1 B(1;a+1) AD = a−2 BC = a+1−2 = a−1 h=1

	a−1+a−2		2a−3
P=		*1 =
	2		2

został jeszcze przypadek a∊(3;4)

Basia: tak; załapałeś czyli już skończysz potem to zebrać "do kupy" i opisać P(a)

michal: W takim razie bardzo dziękuję za super wyczerpującą pomoc!