... Agata:): Punkt O jest srodkiem okregu opisanego na trojkacie ABC. Poprowadziono wysokosc CD trojkata. Wykaz, ze kat ACD=kąt BCO.

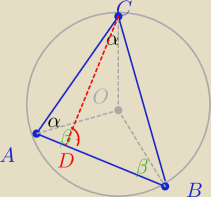
iteRacj@: w Δ BCO

	180o−α−α−β−β
∠BCO=<OBC =		= 90o−α−β
	2

w Δ CDA <ACD+<DAC+90^o = 180^o stąd <ACD= 90^o−<DAC <DAC=α+β <ACD= 90^o−α−β ∠ACD=∠BCO c.b.d

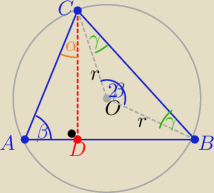
Eta: W Δ prostokątnym ADC α+β=90^o⇒ α=90^o−β W Δ równoramienny BOC |∡BOC|=2β jako kąt środkowy oparty na łuku BC

	180o−2β
zatem jeden z kątów tego trójkąta jest : γ=		= 90o−β = α
	2

i mamy tezę