Relacje - przedstaw graficznie
ewa1:
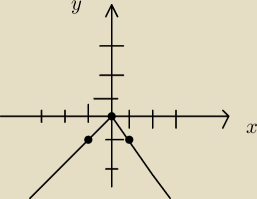
Witam. Mógłby ktoś sprawdzić, czy dobrze rozumiem a jeśli nie, nakierować na właściwy sposób
rozumowania?

Otóż mam takie zadanie: przedstaw graficznie relacje R w zbiorze liczb rzeczywistych:
a) xRy ⇔ x−y ≥ 1
Czy tak będzie wyglądał ten wykres?
Mam też sprawdzić, czy relacja jest zwrotna, symetryczna lub przechodnia.
1) Zwrotna − tak
xRx
x−x ≥ 1
np. 1−1≥1
2) Symetryczna − nie
xRy ⇔ yRx
x−y≥1
y−x≥1
sprzeczność
3) Przechodnia − nie
x−y≥1
y−z≥1
dodaję stronami:
x−z≥2
16 sty 12:36
PW:
x−y≥1
y≤x−1
Zbiór punktów spełniających równanie
(1) y=x−1
to prosta − wykres funkcji liniowej − nic się nie zmieniło od gimnazjum. Punkty, dla których
y<x−1
leżą poniżej (jest to półpłaszczyzna, której krawędzią jest prosta (1)).
Relacja nie jest zwrotna. Sam napisałeś:
x−x≥1
− toż to zdanie fałszywe dla każdego x.
Relacja jest przechodnia. Skoro − jak słusznie zauważyłeś −
x−z≥2,
to tym bardziej
x−z≥1.
16 sty 13:39
ewa1: Przepraszam, mój błąd

Mógłbyś mi jeszcze sprawdzić to:
|x|<y
1) zwrotna − nie |x|<x
2) symetryczna − nie
|x|<y
|y|<x
3) przechodnia
|x|<y
|y|<z
|x|<z tak
16 sty 14:12
 Witam. Mógłby ktoś sprawdzić, czy dobrze rozumiem a jeśli nie, nakierować na właściwy sposób
rozumowania?
Witam. Mógłby ktoś sprawdzić, czy dobrze rozumiem a jeśli nie, nakierować na właściwy sposób
rozumowania?  Otóż mam takie zadanie: przedstaw graficznie relacje R w zbiorze liczb rzeczywistych:
a) xRy ⇔ x−y ≥ 1
Czy tak będzie wyglądał ten wykres?
Mam też sprawdzić, czy relacja jest zwrotna, symetryczna lub przechodnia.
1) Zwrotna − tak
xRx
x−x ≥ 1
np. 1−1≥1
2) Symetryczna − nie
xRy ⇔ yRx
x−y≥1
y−x≥1
sprzeczność
3) Przechodnia − nie
x−y≥1
y−z≥1
dodaję stronami:
x−z≥2
Otóż mam takie zadanie: przedstaw graficznie relacje R w zbiorze liczb rzeczywistych:
a) xRy ⇔ x−y ≥ 1
Czy tak będzie wyglądał ten wykres?
Mam też sprawdzić, czy relacja jest zwrotna, symetryczna lub przechodnia.
1) Zwrotna − tak
xRx
x−x ≥ 1
np. 1−1≥1
2) Symetryczna − nie
xRy ⇔ yRx
x−y≥1
y−x≥1
sprzeczność
3) Przechodnia − nie
x−y≥1
y−z≥1
dodaję stronami:
x−z≥2
 Mógłbyś mi jeszcze sprawdzić to:
|x|<y
1) zwrotna − nie |x|<x
2) symetryczna − nie
|x|<y
|y|<x
3) przechodnia
|x|<y
|y|<z
|x|<z tak
Mógłbyś mi jeszcze sprawdzić to:
|x|<y
1) zwrotna − nie |x|<x
2) symetryczna − nie
|x|<y
|y|<x
3) przechodnia
|x|<y
|y|<z
|x|<z tak