proszę o rozwiązanie Anna: wyznacz dziedzinę i zbiór wartości funkcji

	2x − 1
f(x) =
	Ix +2I − 1

Jerzy: Dziedzinę wyznacz z warunku: |x + 2| − 1 ≠ 0

Anna: to wyznaczyła i mój wynik to x ∊ R \ { −1 ;−3} ale nie wiem jak zbiór wartości

Anna:

	2x−1		2( Ix +2I −1) − 3		3
		=		= 2 −
	Ix+2I −1		I x + 2I −1		I x + 2I −1

czyli Zw = (2 ; +∞) czy to jest dobrze

Jerzy: Rozpatruj oddzielnie w przedziałach.

Anna: niestety nie wiem jak to zrobić

Jerzy:

	2x − 1
Dla: x + 2 < 0 , masz funkcję: f(x) =
	−x − 2 − 1

	2x − 1
Dla: x + 2 ≥ 0 , masz funkcję: f(x) =
	x + 2 − 1

Jerzy: Nie zapomnij też,o asymptotach pionowych: x = −1 oraz x = − 3

Anna: narysowałam układ współrzędnych asymptoty pionowe x = −1 i x=−3 asymptoty poziome y = − 2 i y = 2 dalej nie wiem jak będzie wyglądał wykres

Anna: czy zbiór wartości jest taki jak 14.06

Basia:

	2x−1
f(x) =
	|x+2|−1

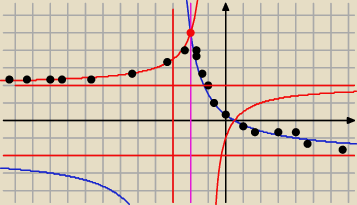
x∊R\{−1; −3} x∊(−∞; −3)∪(−3;−2) ⇒ |x+2|=−x−2 i masz

	2x−1		2(x−(1/2))		2(x+3−3−{1/2})
f(x) =		= −		= −		=
	−x−3		x+3		x+3

	2(x+3) − (7/2)		2(x+3) − 7		7
−		= −		=		−2
	x+3		x+3		x+3

niebieska krzywa tylko w przedziale od (−∞; −3)∪(−3;−2) x∊<2,−1)∪(−1;+∞) ⇒ |x+2| =x+2 i masz

	2x−1		2(x+1)−3		3
f(x) =		=		= −		+ 2
	x+1		x+1		x+1

czerwona krzywa tylko w <2,−1)∪(−1;+∞) tego co jest wykropkowane na czarno nie ma ZW_f = (−∞;−2)∪(−2;2)∪(2;+∞)

Basia: tu masz taki trochę ładniejszy https://www.matemaks.pl/program-do-rysowania-wykresow-funkcji.html

Basia: ale musisz sama wprowadzić wzór funkcji

Anna: dziękuję bardzo