planimetria MatMal: dany jest rownoleglobok abcd o kacie ostrym roznym od 60 na bokach bc i cd zbudowano trojkaty rownoczone BCM i DCN udowodnij ze trojkat AMN jest rownoboczny siedze juz i siedzie nad tym zadaniem i dalej nie wiem czego sie zlapac

iteRacj@: https://www.matematyka.pl/140522.htm

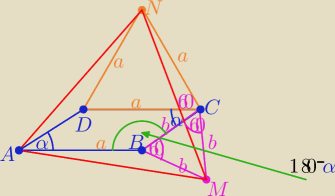
Eta: |<MCN|=120+α i |<ABC|=|<ADC|=180−α| to |< ABM|=360−(180−α+60) =120+α=|<ADN| zatem trójkąty ABM i MCN i ADN są przystające z cechy (bkb) więc |AN|=|AM|=|MN| więc trójkąt AMN jest równoboczny c.n.u

Eta:

MatMal: Nie pomyslalem zeby to narysowac orzestrzennie i dlatego rysunek za azdym razem byl takido kitu,dzieki wielkie

Eta: 2 sposób

	α		α
|<NMC|=|<MNC|= 60+		i |<AMB|= |<MAB|= 60+
	2		2

to |<AMN|= 60^o i analogicznie z pozostałymi kątami ....................... zatem ΔAMN jest równoboczny