Zespolone Pomocy: 1.Niech z0, z1...z4 będą pierwiastkami algebraicznymi stopnia 5 z 32 oblicz ∑od k=0 do 4 z |2i−zk|² 2.Wiedząc, że z jest liczbą zespoloną o argumencie głównym alfa∊(π/2,π) oraz o module |z|>1 znajdź argument główny liczby zespolonej ([sprzężone(−iz)]z³)/(1−|z|²)

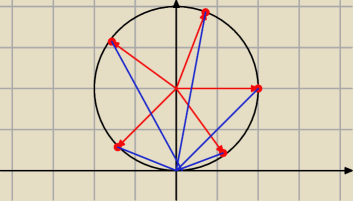
g: 1. Trzeba zsumować kwadraty długości niebieskich odcinków. 2. arg(−iz) = alfa − π/2 arg((−iz)^*) = −(alfa − π/2) arg((−iz)^*z³) = −(alfa − π/2) + 3*alfa arg(1−|z|²) = π arg(wszystko) = −(alfa − π/2) + 3*alfa − π = 2*alfa − π/2