Ciag rozbiezny
Ariel: Ciag (a
n) okreslony nastepujaco jest
wykazac ze jest rozbiezny
mam dwa podciagi
1) a
n'k= a
2k
2) a
n''k= a
4k+1
Po podstawieniu wyjda rozne granice tzn 0 i 1
Dlaczego akuratnie takie podciagi ? czy mozna dobrac inne ?
12 sty 18:42
kochanus_niepospolitus:
może wybrać inne, tylko:
a2k = 0 (dla dowolnego k)
a4k+1 = 1
a4k+3 = −1
ogólnie ... ciąg ten przyjmuje tylko 3 wartości (−1, 0 i 1)
12 sty 18:46
Ariel: A takze
jakie dobrac podciagi do takiego ciagu
| | π | |
an= cos n |
| aby wykazac ze jest rozbiezny? |
| | 2 | |
12 sty 18:47
kochanus_niepospolitus:
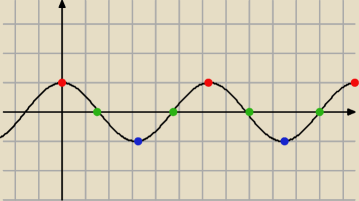
prawie takie same
12 sty 18:52
Ariel: kochanusniepospolitus
to a2k to rozumiem ze to sa n parzyste
Wiec dlaczego nie moze byc a2k+1 zamiast a4k+1
to rozumiem ze ma byc dla n nieparzystych .
Mozesz napisac inne podciagi do 1 przykladu ?
12 sty 18:55
kochanus_niepospolitus:
podciąg: a2k+1 przyjmuje dwie wartości na przemian: 1 i −1
taki podciąg nie jest zbieżny.
12 sty 18:57
kochanus_niepospolitus:
inne podciągi:
a4k i a4k+1
12 sty 18:58
kochanus_niepospolitus:
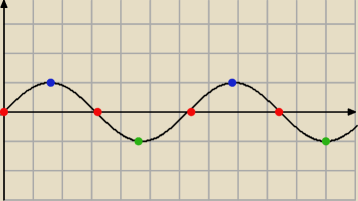
12 sty 19:00
Ariel: Myslalem nad tym i dla a
2k+1byloby
| | π | | π | |
an= sin(2k+1)* |
| = sin(kπ+ |
| ) a to jest tak jak piszesz ze nie jest zbiezny |
| | 2 | | 2 | |
Dzieki bardzo
12 sty 19:05
kochanus_niepospolitus:
najlepiej sobie wybrać w takich przypadkach dwa podciągi takie, które będą już zbieżne, ale do
różnych granic.
wybranie a
2n+1 otrzymasz ciąg który nie jest zbieżny, a aby to wykazać będziesz musiał znowu
wybrać podciągi tego podciągu

Zupełnie zbyteczna 'zabawa'

12 sty 19:08
Ariel: Mam tez przy granicach funkcji wybrac podciagi ale to pozniej sie zgloszse do tablicy

Teraz ciagi .
12 sty 19:12
 prawie takie same
prawie takie same

 Zupełnie zbyteczna 'zabawa'
Zupełnie zbyteczna 'zabawa' 
 Teraz ciagi .
Teraz ciagi .