W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej ma długość d i
Ilna: W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej ma długość d i tworzy z
sąsiednią ścianą kąt α. Wyznacz wysokość tego graniastosłupa. Uzasadnij, że zadanie ma
rozwiązanie dla α<60
12 sty 18:00
kochanus_niepospolitus:
d =
√a2 + h2 ⇒ d > h (1)
z tw. cosinusów:
h
2 = d
2 + d
2 − 2d
2cosα ⇔ h
2 = 2d
2(1−cosα) (2)
z (1) wynika, że:
| | 1 | |
h2 = 2d2(1−cosα) < d2 ⇒ 2(1−cosα) < 1 ⇔ cosα > |
| ⇔ α < 60o |
| | 2 | |
12 sty 18:08
Basia:
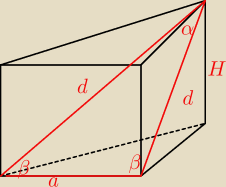
podstawa jest oczywiście trójkątem równobocznym
ściany boczne są prostokątami przystającymi, więc przekątne są równe
z tw.cosinusów
a
2=d
2*d
2−2d*d*cosα
a
2=2d
2(1−cosα)
a
2+H
2=d
2
2d
2(1−cosα)+H
2 = d
2
H
2 = d
2−2d
2(1−cosα)
H
2 = d
2(1−2+2cosα)
H
2=d
2(2cosα−1)
H= d
√2cosα−1
i oczywiście
2cosα−1>0
2cosα>1
α∊(0;60)
12 sty 18:13
kochanus_niepospolitus:
ojjj ... mała pomyłka u mnie ... winno być 'a', a nie 'h' przy tw. cosinusów
12 sty 18:14
Ilna:
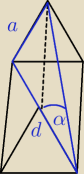
Mógłbyś narysować? Ja próbowałam tak:
a
2 = d
2 + d
2 − 2d
2cosα
12 sty 18:24
Ilna: O, już jest, dziękuję.
12 sty 18:25
kochanus_niepospolitus:
no i bardzo dobrze kombinujesz
założenie: d>a
i napisane przez Ciebie tw. cosinusów ... to wystarczy na wykazanie, że α < 60o
12 sty 18:25
Basia: @szanowna llno może tak ruszyć mysz, przewinąć stronę do góry i przeczytać wcześniejsze
posty?
12 sty 18:29