ekstremum fonkcji zaanetad: Wyznaczyć ekstremum funkcji i zbadaj jej monotoniczność f(x) = √1 − 4x²

zaanetad: Chodzi mi głównie o to jak policzyć pochodną z takiej funkcji

Jerzy: Ustal dziedzinę.

	−4x
f'(x) =
	√1 − 4x2

zaanetad: Dziedzina będą x>0 A skąd ta pochodna, byłabym wdzięczna za wytłumaczenie

Basia: dziedzina niepoprawna jakie musi być wyrażenie,które jest pod pierwiastkiem parzystego stopnia?

5-latek:

	1
f'(x)=		*(1−4x2)'=
	2√1−4x2

zaanetad: x∊(−∞;−¹₂) lub (¹₂;∞) tak?

Jerzy: To pochodna funkcji złożonej, gdzie funkcją wewnętrzną jest funkcja: g(x) = 1 − 4x², a jej pochodna: g'(x) = −8x ( nedruje do licznika )

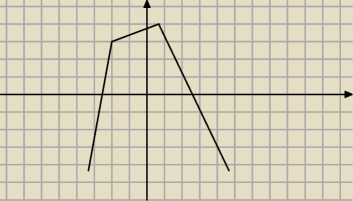
5-latek: Zle . Nie zgaduj tylko wez kartke i policz masz a<0

Jerzy:

	1		1
A dlaczego		i −		nie należą do dziedziny ?
	2		2

Jerzy: Nie zauważyłem,że napisałaś sumę przedziałów , a ma być jeden przedział.

zaanetad: to co pod pierwiastkiem ma być większe od zera tak?

Jerzy: A dlaczego nie może być równe 0 ?

zaanetad: 1−4x²>0 −4x²>−1 x²<¹₄

5-latek: ≥0

zaanetad: A no tak

zaanetad: Czyli z jedną drugą

Jerzy: Jaka jest w końcu wg Ciebie dziedzina ?

zaanetad: D: x∊(−∞;¹₂> suma <¹₂;∞)

Jerzy: Dalej żle. Zrób szkic.

zaanetad: <−¹₂;¹₂> to co nad osią?

Jerzy: Teraz tak.

zaanetad: A jeżeli później wezmę obiczę warunek dostateczny czyli f'(x)>0 oraz f'(x)<0 jak mam narysować wykres?

Jerzy: Wykres czego ?

zaanetad: f'(x)>0 znalazłam taki pierwiastek x=0, co dalej z tym zrobić?

Jerzy: Jak zmienia sie znak pochodnej w punkcie x = 0 ?

zaanetad: właśnie nie umiem tego sprawdzić

Jerzy: Zanak zależy tylko od znaku licznika, bo mianownik jest dodatni.