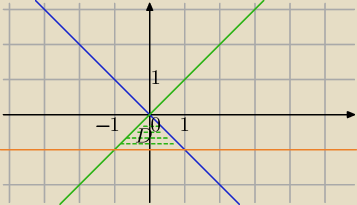
całka podwójna Monika: Obliczyć ∫∫(y+1)dxdy Pole ograniczone przez : y=−x, y=x, y=−1 y≤x≤−y −1≤y≤0 ∫⁰₋₁ dy ( ∫^−y_y (y+1) dx ) = ∫⁰₋₁ (−2y)(y+1) dy = 1/3 Tak rozwiązałam do zadanie w duzym skrócie. niestety po wykresie wnioskuję, że pole trójkąta 1/2(ah)=1/2(2*1)=1 Gdzie jest błąd w moim mysleniu?

Jerzy: Zacznij od poprawnego ustalenia granic całkowania.

Mila: Pole obszaru za pomocą podwójnej całki: P=2*₀∫¹[₋₁∫^y=−xdy]dx=

	1
=2*(0∫1[y]−1−x)dx=20∫2(−x+1)dx=2*[−		x2+x]01=
	2

	1		1
=2*[−		+1−0)=2*		=1
	2		2

Natomiast taka całka podwójna: ∫∫_D(y+1)dxdy= za chwilę

Mila: Interpretacja geometryczna całki podwójnej. http://edu.pjwstk.edu.pl/wyklady/am/scb/index112.html

Mila: ∫∫D(y+1)dxdy=₋₁∫⁰[₋₁∫^y=x(y+1)dy] dx+₀∫¹[₋₁∫^y=−x(y+1)dy] dx=

	1
=
	3