trapez Maciek: W trapez równoramienny o obwodzie 52 wpisano okrąg Odcinek łączący środki przekątnych ma długość 5 Oblicz długość odcinka łączącego punkty styczności okręgu z ramionami trapezu

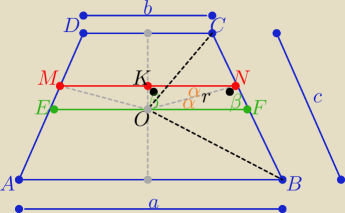
Eta: |MN|= ? Z warunku wpisania okręgu w trapez a+b=2c i z treści zadania ⇒ 2a+2b=52 ⇒ a+b=26

	a−b
oraz		= 5 −− dł. odcinka łączącego środki przekątnych trapezu
	2

zatem: a+b=26 i a−b= 10 + −−−−−−−−−− 2a=36 ⇒ a=18 i b=8 to |CN|=4 i |BN|=9 w ΔBOC : r²=4*9 =36

	a+b
oraz |EF|=		−−− dł. środkowej trapezu ⇒ |EF|=13 to |OF|=6,5
	2

trójkąty ONK i ONF są podobne z cechy (kkk)

	|KN|		r		r2		36
zatem:		=		⇒ |KN|=		=
	r		|OF|		|OF|		6,5

	72		144		1
to |MN|=2|KN|=		=		=11
	6,5		13		13

	1
Odp: |MN|=11
	13

================

Maciek: Dzięki wielkie Eta