Nieskonczenie male funkcji rownowaznych
5-latek: Nieskonczenie małe funkcji rownowaznych
α(x)− nieskonczenie male gdy x→0
mamy wtedy
| | α(x) | |
[1+α(x)]p−1 ∼pα(x) w szczegolnosci n√1+α(x)−1∼ |
| |
| | n | |
sinα(x)∼α(x)
Wykazac ze
c) sin
√x√x ∼
√x2+√x3
12 sty 11:06
5-latek: Zapomnialem dopisac ze dla x→0 .
12 sty 11:09
5-latek: Przepraszam ale muszse wyjechac wiec jesli ktos odpowie to proszse sie nie denerowac ze nie
odpisuje .
12 sty 11:18
Adamm: a) α(x)=x
p=−1/2
mamy że
b) α(x)=x
p=−1
mamy
c) coś chyba źle przepisane
12 sty 14:51
5-latek:
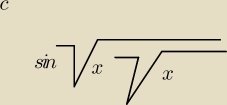
Czesc
Mozesz a i b lepiej wytlumaczyc?
12 sty 14:55
Adamm: stosujesz ten wzór który podałeś
jak pomnożysz obie strony przez stałą (w tym przypadku −1), to nic się wcale nie zmieni
12 sty 15:00
Adamm: może się coś zmienić jeśli ta stała jest = 0, ale poza tym to nie
12 sty 15:01
5-latek: Dobrze . dzieki .
12 sty 15:02
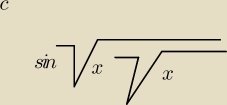 Czesc
Mozesz a i b lepiej wytlumaczyc?
Czesc
Mozesz a i b lepiej wytlumaczyc?