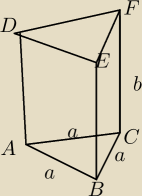
stereometria - liceum, rozszerzenie house: Suma długości wszystkich krawędzi graniastosłupa prawidłowego trójkątnego jest równa 9. Oblicz wymiary graniastosłupa, który ma objętość największą z możliwych. 6a+3b=9 => b=3−2a

	a2√3		3a2√3−2a3√3
V=		*(3−2a)=
	4		4

	6√3a(2a3√3)−6√3a2(3a2√3)		36a4−54a4
V'(a)=		=
	16		16

raczej nie powinno tak wyjść odpowiedź to 1

Eta: b=3−2a , a∊(0,3/2)

	3a2√3		a3√3
V=		−
	4		2

	3		√3		3√3a		3√3a2
V'(a)=		√3*2a −		*3a2=		−
	4		2		2		2

V^'(a)=0 ⇒ .............. ⇒ a−a²=0 ⇒ a(1−a)=0 ⇒ a=1 .................. i jeszcze uzasadnij ,że dla a=1 V(a) osiąga maksimum

house: to już easy, ramiona paraboli są skierowane w dół, czyli na wykresie przy a=1 zmienia się znak z + na −, czyli jest tam maksimum. Dziękuję bardzo