stereometria - liceum, rozszerzenie
house:
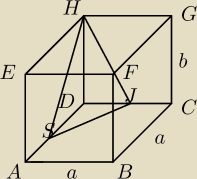
Odcinek o długości d łączy środek krawędzi podstawy z dowolnym wierzchołkiem drugiej podstawy
graniastosłupa prawidłowego czworokątnego.
Oblicz wymiary graniastosłupa, który ma pole powierzchni bocznej największe z możliwych.
SD=DJ=d=0,5a
z trójkąta SDJ −> a=d
√2
nie wiem, jak uzależnić b od d
11 sty 21:34
iteRacj@:
odcinkiem łączącym środek krawędzi podstawy z dowolnym wierzchołkiem drugiej podstawy jest
również SG lub SF, a te odcinki mają inną długość niż SH i SE
czy ja dobrze to widzę?
11 sty 22:05
Basia: przecież SH i HJ nie muszą być prostopadłe
iteRacj@ dobrze widzisz
11 sty 22:15
iteRacj@:
dzięki
11 sty 22:16
house: Faktycznie muszę kilka przypadków rozważyć,
jutro zerknę na to zadanie ponownie, może coś więcej wypatrzę.
11 sty 22:32
Basia:
dane: d
w przypadku takim jak na rysunku mamy b∊(0

)
4d
2=a
2+4b
2
a
2 = 4d
2−4b
2 = 4(d
2−b
2)
a = 2
√d2−b2
P
b = 4ab = 8b
√d2−b2=f(b)
i trzeba znaleźć maksimum tej funkcji
| | 1 | |
f'(b) = 8√d2−b2+ |
| *8b*(−2b) = |
| | 2√d2−b2 | |
| | b | | d2−b2−b | | −b2−b+d2 | |
8[ √d2−b2 − |
| ]= 8* |
| =8* |
| |
| | √d2−b2 | | √d2−b2 | | √d2−b2 | |
| | 8 | |
miejsca zerowe i znak pochodnej zależą tylko od y=−b2−b+d2 bo |
| jest stale |
| | √d2−b2 | |
dodatni
−b
2−b+d
2=0
Δ=1−4*(−1)*d
2 = 1+4d
2>0
b∊(0;b
2) ⇒ f'(b)>0 ⇒ f rośnie
b∊(b
2; d) ⇒ f'(b)<0 ⇒ f maleje
| | 1+√1+4d2 | |
czyli dla b= |
| osiąga maksimum |
| | 2 | |
należałoby jeszcze sprawdzić czy b
2<d i policzyć a
1+
√1+4d2<2d
√1+4d2<2d−1
1+4d
2<4d
2−4d+1
4d<0
sprzeczność
więc albo się pomyliłam,albo w tym przypadku zadanie nie ma rozwiązania
11 sty 22:51
Basia:
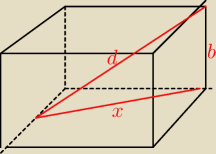
przypadek2
4d
2 =5a
2+b
2
b
2 = 4d
2−5a
2
b =
√4d2−5a2
f(a) = P
b = 4ab = 4a*
√4d2−5a2
| | 1 | | 4d2−5a2+a | |
f'(a) = 4[ √4d2−5a2+a* |
| ) = 4* |
| |
| | 2√4d2−5a2 | | 2√4d2−5a2 | |
−5a
2+a+4d
2=0
Δ=1−4*(−5)*4d
2 = 1+20d
2>0
oczywiście w a
2 byłby maksimum, ale znowu pytanie czy
−1+
√1+20d2<2d
√1+20d2<2d+1
1+20d
2<4d
2+4d+1
16d
2−4d<0
4d(d−4)<0
d<4
tak jest to możliwe dla d<4
| | 1+20d2 − 2√1+20d2+1 | | 2+20d2−2√1+20d2 | |
a2 = |
| = |
| |
| | 4 | | 4 | |
| | 10+100d2−10√1+20d2 | |
b2 = 4d2− |
| = |
| | 4 | |
| 16d2−10−100d2+10√1+20d2 | | −84d2−10+10√1+20d2 | |
| = |
| |
| 4 | | 4 | |
ten ułamek musiałby być dodatni
sprawdzam czy jest
−84d
2−10+10
√1+20d2>0
10
√1+20d2>84d
2+10 /:2
5
√1+20d2>42d
2+5
15(1+20d
2)>1764d
4+210d
2+25
15+300d
2>1764d
4+210d
2+25
1764d
4−90d
2+10>0 /:2
882d
4−45d
2+5>0
Δ=2015−17640<0
czyli dobrze to jest stale dodatnie
| | −84d2−10+10√1+20d2 | | (−84d2−10+10√1+20d2)1/2 | |
b=( |
| )1/2 = |
| |
| | 4 | | 2 | |
d<4
dla d≥4 zadanie nie ma rozwiązania
12 sty 03:35
Basia: dziwaczne te wyniki; nie wiem czy to jest aby na pewno dobrze policzone
12 sty 03:36
Basia: house skąd masz to zadanie?
12 sty 03:38
house: od mojej matematyczki dla przygotowania przed sprawdzianem, dzięki za próbę,
spróbuję przeanalizować Twoje działania
13 sty 12:01
house: Na początku źle zrozumiałem zadanie, przeczytałem, że odcinek d łączy środki w podstawie

po wrzuceniu pod jeden pierwiastek Pb=
√16a2d2−4a3
f(a)=16a
2d
2−4a
3
f'(a)=32d
2a−18a
2 <−> a=0 v a=2d
2
Pb(2d
2)=
√16*4d4d2−32d6=4
√2d
jest ok?
14 sty 14:43
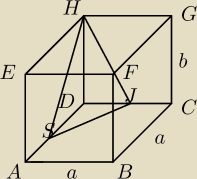 Odcinek o długości d łączy środek krawędzi podstawy z dowolnym wierzchołkiem drugiej podstawy
graniastosłupa prawidłowego czworokątnego.
Oblicz wymiary graniastosłupa, który ma pole powierzchni bocznej największe z możliwych.
SD=DJ=d=0,5a
z trójkąta SDJ −> a=d√2
nie wiem, jak uzależnić b od d
Odcinek o długości d łączy środek krawędzi podstawy z dowolnym wierzchołkiem drugiej podstawy
graniastosłupa prawidłowego czworokątnego.
Oblicz wymiary graniastosłupa, który ma pole powierzchni bocznej największe z możliwych.
SD=DJ=d=0,5a
z trójkąta SDJ −> a=d√2
nie wiem, jak uzależnić b od d
 )
)
 przypadek2
przypadek2
