udowodnij że nie istnieje stożek w którym pole powierzchni całkowitej jest trzy krystian prosi o pomoc: udowodnij że nie istnieje stożek w którym pole powierzchni całkowitej jest trzy razy większe od pola jego przekroju osiowego

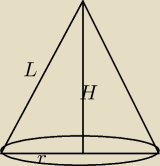
Basia: P_c = πr²+πrL P_przekroju = ¹₂*2r*H = r*H gdyby πr²+πrL = 3*r*H /:r to πr+πL = 3H

	π(r+L)
H =
	3

z tw.Potagorasa r²+H²=L²

	π2(r+L)2
r2+		= L2 /*9
	9

9r² + π²(r²+2rL+L²)=L² (9+π²)r²+2π²Lr+L²(π²−1) = 0 traktujemy to równanie jak równanie z niewiadomą r i parametrami π i L Δ = (2π²L)²−4*(9+π²)*L²(π²−1) = 4π⁴L² − 4L²(9π²−9+π⁴−π²) = 4L²(π⁴−9π²+9−π⁴+π²) = 4L²(−8π²+9) Δ≥0 4L² jest >0 czyli −8π²+9≥0 8π²≤9 π²≤⁹₈ sprzeczność bo π²>9 czyli przypuszczenie było fałszywe czyli πr²+πrL ≠ 3*r*H czyli P_c ≠ 3*P_{przekroju osiowego}

krystian prosi o pomoc: πr2+πrL = 3*r*H tak napisalas, a nie powinno byc 3πr2+πrL = r*H

krystian prosi o pomoc: aha Ty masz racje. sorry