całki podwójne Bartek: Całka podwójna − jak liczyć? Witam, bardzo proszę aby ktoś rozpisał mi w miarę krok po kroku jak obliczyć tą całkę: całka podwójna (x+y)dxdy gdzie D: −1<=x<=2 0<=y<=x²+3 Pozdrawiam

Basia: = ∫₋₁²(∫₀^x2+3(x+y)dy)dx =

	y2
∫−12(xy+		|0x2+3)dx=
	2

	(x2+3)2		02
∫−12{x(x2+3)+		−x*0−		)dx =
	2		2

	x4+6x2+9
∫−12(x3+3x +		)dx= .............
	2

dalej wiesz?

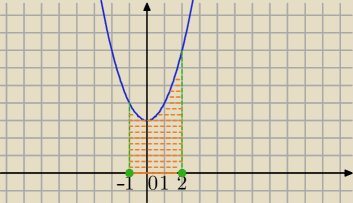Mila: ₋₁∫²[₀∫^y=x2+3(x+y)dy]dx=

	1
=−1∫2([xy+		y2]0x2+3)dx=
	2

	1
=−1∫2[x*(x2+3)+		*(x2+3)2−0]dx=
	2

	1		9
=−1∫2[x3+3x+		x4+3x2+		] dx=
	2		2

	1		1		1		1		1		9
=[		x4+3*		x2+		*		x5+3*		x3+		x]−12=
	4		2		2		5		3		2

	1		1		3		9
=[		x5+		x4+x3+		x2+		x]−12=
	10		4		2		2

	1		1		3		1		1		3		9
=		*32+		*16+8+		*4+9−(−		+		−1+		−		)=
	10		4		2		10		4		2		2

	32		1		1
=		+27−(−4		+		)=
	10		10		4

	681
=
	20