Pole - całka Takosen: Obliczyć pole ograniczone krzywymi y² y=−x+2 y+0 czy to będzie tak wyglądało: ∫(−x+2)− √x− 0)dx w granicach od 0 do 2?

Basia: czy to ma być y²*y = −x+2y+0 jakoś sensu nie widzę napisz to może porządnie

Takosen: y²=x y=−x+2 y=0 Poprawiłem

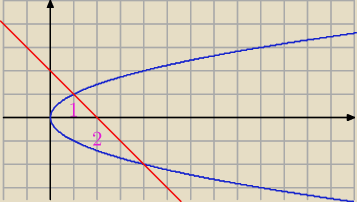
Basia: rozwiązujemy układ y = −x+2 y²=x (−x+2)² = x (2−x)²=x 4−4x+x²=x x²−5x+4=0 Δ=25−16=9 √Δ=3

	5−3
x1=		=1
	2

x₂=4 punkty przecięcia A(1,1) B(4,−2) y²=x y=√x lub y=−√x dodatkowo ograniczeniem jest y=0 czyli oś OX no i tu mam problem ten obszar (2) też jest ograniczony tymi krzywymi i osią OX P₁=∫₀¹√xdx+∫₁²(−x+2)dx P₂ = ∫₀⁴(−√x)dx −∫₂⁴(−x+2)dx tylko broń boże nie P₁+P₂ bo po połączeniu obszar nie spełnia warunków zadania (nie jest ograniczony przez y=0)

Takosen: Czy granica w pierwszym polu nie powinna być od 0 do 2

Takosen: Czy za jednym razem można zrobić od 0 do 2?

Basia: Nie; P₁ składa się z dwóch części: pod niebieską krzywą na <0;1>+pod czerwoną krzywą na<1,2>

Takosen: To jak wyznaczyć granice całkowania w tym zadaniu? Oblicz pole obszaru zawartego pomiędzy parabolą y²=4x i prostą y=2x−4 Bo trochę się pogubiłem