 Cześć przychodzę do was z pewnym problemem, który chodzi mi po głowie. Trójkąt wyżej wynika z
zadania:
Kąt rozwarcia stożka ma miarę 120° , a tworząca tego stożka ma długość 4. Objętość tego
stożka jest równa: ... . Odpowiedź do tego zadania to 8π. Z rozwiązania zadania wychodzi, że
(zaznaczone kolorem niebieskim)
wysokość ma być równa 2 a podstawa 2√3.
Odrazu uprzedzam że wiem że zadanie możnaby policzyć z dorysowania drugiej części trójkąta,
stworzenia równobocznego i wyliczenia wszystkiego,
lecz nie o to w tym chodzi.
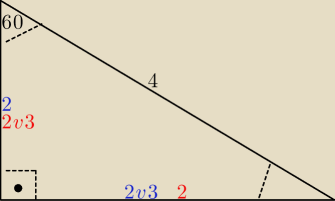
Otóż biorąc za kąt 60 sinα=60, otrzymamy: własność sinα60=a/c, czyli √2/3=a/4 z czego wyjdzie
nam, a równe 2√3, więc licząc następnie z pitagorasa wysokość 2.
I tu rodzi się całe pytanie, skąd wiemy że należy wziąć sinα60 stopni a nie cosβ60 stopni?
Licząc cosβ60=a/c => 1/2=a/4 => a=2 zadanie wyjdzie na odwrót(kolor czerwony na
rysunku)
Proszę o odpowiedź na ten temat, bo nie daje mi to spokoju a myślę, że jest to ważna wiedza.
Cześć przychodzę do was z pewnym problemem, który chodzi mi po głowie. Trójkąt wyżej wynika z
zadania:
Kąt rozwarcia stożka ma miarę 120° , a tworząca tego stożka ma długość 4. Objętość tego
stożka jest równa: ... . Odpowiedź do tego zadania to 8π. Z rozwiązania zadania wychodzi, że
(zaznaczone kolorem niebieskim)
wysokość ma być równa 2 a podstawa 2√3.
Odrazu uprzedzam że wiem że zadanie możnaby policzyć z dorysowania drugiej części trójkąta,
stworzenia równobocznego i wyliczenia wszystkiego,
lecz nie o to w tym chodzi.
Otóż biorąc za kąt 60 sinα=60, otrzymamy: własność sinα60=a/c, czyli √2/3=a/4 z czego wyjdzie
nam, a równe 2√3, więc licząc następnie z pitagorasa wysokość 2.
I tu rodzi się całe pytanie, skąd wiemy że należy wziąć sinα60 stopni a nie cosβ60 stopni?
Licząc cosβ60=a/c => 1/2=a/4 => a=2 zadanie wyjdzie na odwrót(kolor czerwony na
rysunku)
Proszę o odpowiedź na ten temat, bo nie daje mi to spokoju a myślę, że jest to ważna wiedza.
| h | 1 | 1 | |||
= sin 30o = | ⇒ h = 4* | = 2 | |||
| 4 | 2 | 2 |
| h | 1 | 1 | |||
= cos 60o = | ⇒ h = 4* | = 2 | |||
| 4 | 2 | 2 |
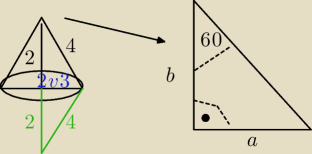 Można dorysować trójkąt pomocniczy (zielony) i wtedy wyjdzie trójkąt równoboczny i wszystkie
boki będą
miały długość 4, czyli wysokość stożka to będzie 2.
Ale bez dorysowywania można narysować obok ten trójkąt ze stożka i wtedy licząc z sinα=60
wychodzi nam
sin60=a/4 => a=2√3 a wysokość b wyliczona po tym działaniu to 2 czyli prawidłowa. I TU
pojawia się
pytanie skąd wiemy że należy wziąć sin60 a nie cos60, który ma taki sam wzór lecz inna wartość
z tablic.
cos60=a/c => a=2, a wysokość b 2√3
Można dorysować trójkąt pomocniczy (zielony) i wtedy wyjdzie trójkąt równoboczny i wszystkie
boki będą
miały długość 4, czyli wysokość stożka to będzie 2.
Ale bez dorysowywania można narysować obok ten trójkąt ze stożka i wtedy licząc z sinα=60
wychodzi nam
sin60=a/4 => a=2√3 a wysokość b wyliczona po tym działaniu to 2 czyli prawidłowa. I TU
pojawia się
pytanie skąd wiemy że należy wziąć sin60 a nie cos60, który ma taki sam wzór lecz inna wartość
z tablic.
cos60=a/c => a=2, a wysokość b 2√3
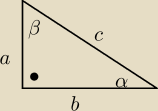 Mam Cię ... powtórz związki trygonometryczne w trójkącie prostokatnym:
Mam Cię ... powtórz związki trygonometryczne w trójkącie prostokatnym:
| a | |
= sinα = cosβ | |
| c |
| b | |
= cosα = sinβ | |
| c |