styczne Maciek:

	1		5
wyznacz wspólne styczne do paraboli f(x)=		x2 oraz okręgu x2+(y+		)2=2
	2		2

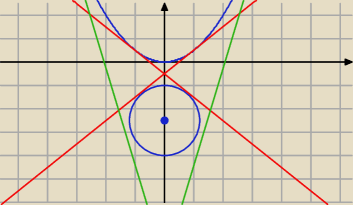
Basia: f'(x)=x czyli współczynnik kierunkowy stycznej w p−cie x₀ jest równy x₀ każda styczna go paraboli ma równanie y=x₀*x+b co wygodniej możemy zapisać tak y= ax+b

	a2
y=f(a)=
	2

a2
	= a2+b
2

	a2
b = −
	2

	a2
k: y=ax−
	2

	a2
k: ax−y−		=0
	2

k: 2ax−2y−a²=0 no i teraz trzeba zbadać dla jakiej wartości parametru a będzie to także styczna do okregu S(0;−⁵₂) r=√2 czyli d(S,k) = √2 U{|2a*0 − 2*(−5/2) − a²|}{√4a²+4 = √2 |5−a²|=2√2*√a²+1 /()² 25−10a²+a⁴ = 8(a²+1) a⁴−18a²+17=0 Δ=18²−4*1*17 = (2*9)² − 4*17 = 4(81−17) = 4*64 √Δ = 2*8=16

	18−16
a2 =		= 1
	2

lub

	18+16
a2=		=17
	2

a=±1 lub a=±√17

	1		1
dla a=±1 b= −U{1}[2} i mamy styczne y=x−		i y=−x−
	2		2

	17		17		17
dla a=±√17 b=−		i mamy styczne y=√17x−		i y=−√17x−
	2		2		2

sprawdź czy się gdzieś w rachunkach nie pomyliłam, ale chyba nie

Mila: Współczynniki a dobrze. Dwa razy liczyłam, bo miałam pomyłkę.

Maciek: a kij z tym, na maturze nie będzie takich zadań, ta matura próbna miała nas tylko wystraszyć

iteRacj@: ładnie Maciek obu paniom podziekowałeś za to liczenie

5-latek: Bo to jest gbur , albo udaje takiego by sie dowartosciowac