Stereometria JacksX: Witam, mam problem z poniższymi zadaniami ze stereometrii. Proszę o pomoc poprzez narysowanie rysunku i wytłumaczenie jak co liczyć, tak bym mógł popróbować sam z obliczeniami. 1. W graniastosłupie prawidłowym czworokątnym przekątna graniastosłupa o długości 12 tworzy z podstawą kąt o mierze 45 stopni. Oblicz objętość oraz pole powierzchni całkowitej tego graniastosłupa. 2. Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 7√2. Przekątna ściany bocznej tworzy z podstawą kąt o mierze 60 stopni. Oblicz: a) pole powierzchni bocznej graniastosłupa b) objętość graniastosłupa c) długość przekątnej graniastosłupa. 3. Oblicz objętość i pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym długść podstawy ma 4 cm, a długość przekątnej graniastosłupa jest równa 2√13 cm. 4. Dany jest graniastosłup prawidłowy trójkątny, w którym długość wysokości podstawy trójkąta jest równa 4√2, a wysokość graniastosłupa stanowi 150% długości jego krawędzi podstawy. Oblicz: a) pole powierzchni całkowitej graniastosłupa b) objętość graniastosłupa 5. W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są równej długości. Wiedząc, że wysokość trójkąta pdstawy ma 7,5 cm długości, oblicz pole powierzchni bocznej tego graniastosłupa. 6. W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej o długości 10 tworzy z podstawą kąt o mierze 60 stopni. Oblicz pole powierzchni bocznej oraz objętość tego graniastosłupa. 7. Podstawa graniastosłupa prostego jest rombem o przekątnych długości 4 i 12. Wysokość graniastosłupa jest równa 3√2. Oblicz pole powierzchni bocznej i objętość graniastosłupa. 8. Najdłuższa przekątna graniastosłupa prawidłowego sześciokątnego o długości 5√6 tworzy z podstawą kąt o mierze 30 stopni. Oblicz: a) pole powierzchni całkowitej graniastosłupa b) objętość graniastosłupa 9. Przekątna podstawy ostrosłupa prawidłowego czworokątnego ma długość 14 cm, a wysokość ostrosłupa jest równa 7√2 cm. Oblicz: a) długości krawędzi podstawy i krawędzi bocznej b) tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy c) objętość i pole powierzchni całkowitej ostrosłupa Pozdrawiam.

5-latek: Nietety musisz sam nauczyc sie robic rysunki do zadan z estereometrii https://matematykaszkolna.pl/strona/3424.html Tutaj masz pomoc . jak klikniesz na zadania to masz tez rysunek do niego

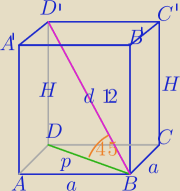
Mila: 1) p=a√2 2) ΔD'DB− Δprostokatny równoramienny. Licz

JacksX: sin45 = H/12 √2/2 = H/12 /*12 √2/2 * 12 = H H = 6√2 cm H² + p² = d² (6√2)² + p² = 12² 72 + p² = 144 p² = 144 − 72 p² = 72 p = √72 p = 6√2 d = a√2 6√2 = a√2 /: √2 a = 6/√2 * √2/√2 = 6√2/2 = 3√2 Pp = a² = (3√2)² = 18 V = Pp * H = 18 * 6√2 = 108√2 Tak zacząłem liczyć, ale wyniki mi się coś nie pokrywają. Powinno wyjść V = 216√2, a Pc = 36(1+4√2)