Udowodnić, że wskazane rozw jest jedyne. asia kozlow: Znajdź dwie liczby naturalne m < n takie, że mⁿ = n^m i udowodnij, że wskazane rozwiązanie jest jedyne. Wiadomo m=2 n=4 ale jak to udowodnić?

asia kozlow: Zadanie z analizy, mamy do dyspozycji szeregi, pochodne, całki itp.

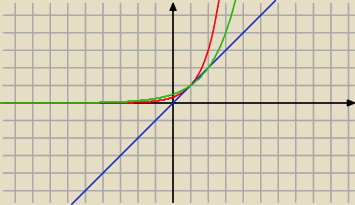
Adamm: mⁿ=n^m (m, n)=d m=m'd, n=n'd (m', n')=1 dⁿ(m')ⁿ=d^m(n')^m d^n−m(m')ⁿ=(n')^m musi być m'|n' a zatem skoro (m', n')=1, więc m'=1 (d^n'−1)^d=(n')^d d^n'−1=n' jeśli d≥3 to d^n'−1≥3^n'−1>n' (patrz wykres czerwony i niebieski; n'>1) czyli musi być d=2 2^n'−1=n' a zatem n'=2 (patrz wykres zielony i niebieski; n'>1) czyli m=2, n=4 to jedyne rozwiązanie

Adamm: zapomniałem jeszcze może być d=1 wtedy n'=1 czyli m=n a tego nie chcemy

jc: x>0, funkcja x → x^1/x rośnie do e (sprawdź lepiej), a potem maleje Dla n > m ≥ 3, m^1/m < n^1/n, czyli mⁿ < n^m. Coś jeszcze trzeba dodać i będzie dowód.

jc: Niejasno napisałem. Max mamy dla x=e.

asia kozlow: Dzięki. Kurde ciężko mi to wykombinować, zaczęłam robić jakieś pojedyncze założenia żeby później dały mi sprzeczność dla innej pary niż 2,4 , ale słabo to wychodziło.

jc: Sam dodam. Pozostają 2 przypadki m=1 oraz m=2. 1¹ < nⁿ dla n>1. Zostaje więc m=2. 2^1/2>5^1/5 bo 2⁵ = 32 > 5²=25 (dla większych n tym bardziej). Należy jeszcze sprawdzić n=3 i n=4. Dla n=3 nie mamy równości, a dla n=5 mamy i jest jedyne rozwiązanie.

jc: W drugiej linii miało być 1ⁿ < n¹.