Styczne do okręgu wixa04: Z punktu P(−1,13) poprowadzono dwie styczne do okręgu (x−2)² + (y−4)² = 9. Oblicz odległość między punktami styczności.

5-latek: Odleglosc miedzy punktami stycznosci wedlug mnie jest rowna srednicy okregu .

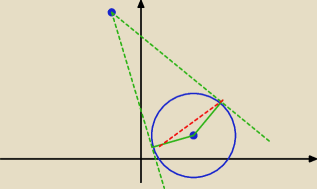
iteRacj@: witaj 5−latku odległość nie będzie równa średnicy

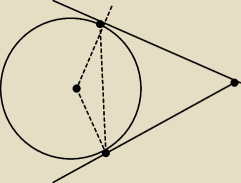
5-latek: napisalem bzdure

5-latek: Dzien dobry iteRacjo

iteRacj@: ale dzięki Twojemu rysunkowi widać, że będzie równa dwóm wysokościom trójkąta i widać którego Δ

iteRacj@: @wixa04 1. proste styczne do okręgu mają równania Ax+By+C=0 i należy do nich P(−1,13) , z tego wylicz C 2. odległość środka okręgu od szukanych punktów styczności jest równa promieniowi i okręgu, to pozwoli znaleźć A i B 3. teraz wylicz współrzędne punktów styczności 4. i zostaje obliczyć odległość pomiędzy nimi czyli wzór na odległość między punktami

5-latek: Srodek okregu S(2,4) Odleglosc punktu P(−1,13) od punktu S

	√90
d= P{32+(−9)2}= √90 czyli r nowego okregu r=
	2

	1		17
Srodek odcinka SP=(		,		)
	2		2

Chcialem to zrobic iteRacjo z konstrukcji elelmntarnej stycznej do okregu ale wyjda troche brzydkie obliczenia Bo nowy okrag bedzie mia rownanie

	17		90
(x−0,5)2+(y−		)2=
	2		4

Jednak do czego zmierzam Przyrownujac te dwa rownania okregow do siebie wyznaczymy punkty stycznosci Przyjmujac na chwile ze ten drugi okrag ma rownanie ladniejszse powiedzmy takie (x−1)²+(y−8)²= 25 WIec tak Rowmie okregu w zadaniu bylo takie (x−2)²+(y−4)²=9 Wyznaczone (x−1)²+(y−8)²=25 Przepisze jeszcze raz {(x−2)²+(y−4)²=9 {(x−1)²+(y−8)²=25 Jak z tego ukladu wyznaczyc punkty stycznosci ?

iteRacj@: ja nie wiem, dlaczego jest liczony nowy okrąg?

5-latek: Za chwile wstawie skan .

iteRacj@: wygląda to na zadanie, którego jednym z celów może być sprawdzenie, czy uczeń bierze pod uwagę, że styczna do okręgu może być prostopadła do osi OX

5-latek: https://zapodaj.net/f8edc9ed38d41.jpg.html

5-latek: Przepraszam ale to nie to Zaraz poprawie

5-latek: https://zapodaj.net/958fae09eeb28.jpg.html iteracjo teraz powinno byc dobrze

iteRacj@: Opisany na zdjęciu sposób jest dobry, gdybyśmy nie chcieli korzystać z tego, że okrąg jest narysowany w układzie współrzędnych. To zadanie sprawdza umiejętności z geometrii analitycznej, więc warto wybrać krótki sposób rozwiązania oparty na znanych uczniom wzorach. Dlatego podany o 13:31 sposób będzie znacznie krótszy. A jesli chodzi o Twoje pytanie dotyczące znalezienia współrzędnych punktów wspólnych dwóch okręgów (13:35), to po prostu trzeba rozwiązać ten układ równań.

5-latek: Wlasnie jak iteRacjo

iteRacj@: podnieś w obu równaniach do kwadratu nawiasy i odejmij stronami, wyrazy w kwadracie się zredukują i wygląda na to, że wynik będzie szybko

iteRacj@: *odejmij stronami oba równania od siebie

5-latek: Pozniej sprobuje zrobic . dzieki

5-latek: No to odejmuje drugie od pierwszsego (x−1)²−(x−2)²+(y−8)²−(y−4)²=16 x²−2x+1−(x²−4x+4)+y²−16y+64−(y²−8y+16)=16 2x−3−8y+48=16 2x−8y= 16−45=29 2x−8y=29 Chce wyznaczyc punkty przeciecia sie tych okregow opisanych tymi rownaniami z 13 : 35 Teraz co dalej ? Wyznaczyc z tego x i wstawic np do 1 rownania i wyznaczyc y ? Jesli tak to troche beda rachunki niemile ale chodzi o algorytm .

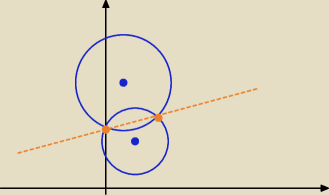
iteRacj@: trzeba rozwiazywać dokładnie tak, jak piszesz punkty wspólne obu okregów leżą na prostej, której równanie wyliczyłeś trzeba wyliczyć z niego jedną zmienną i wstawić, do równania ktoregokolwiek z okręgów

5-latek: Dobry wieczor

iteRacj@: tak, wieczór z geometrią analityczną to dobry wieczór

Basia: Proponuję jeszcze inny sposób. A, B punkty styczności SA^→⊥PA^→ |SA|=r P(−1,13) S(2,4) r=2 pr. PS

	4−13		−9
A =		=		=−3
	2+1		3

y= ax+b 4=2a+b 13=−a+b 2a+b=4 a−b=−13 −−−−−−−−−−−−−−− 3a = −9 a=−3 b=16 y = −3x+16 3x+y+16=0 SA^→ = [3k, k] √9k²+k² =3 10k²=9

	9
k2=
	10

	3√10
k = ±
	10

	9√10		3√10
SA→[		;		]
	10		10

lub

	9√10		3√10
SA→[−		; −		]
	10		10

SA^→[x−2; y−4]

	9√10
x−2 =
	10

	3√10
y−4 =
	10

lub

	9√10
x−2 = −
	10

	3√10
y−4 = −
	10

	20+9√10
x=
	10

	40+3√10
y=
	10

lub

	20+9√10
x=−
	10

	40+3√10
y=−
	10

	20+9√10		40+3√10
A(		;		)
	10		10

	20+9√10		40+3√10
B(−		;−		)
	10		10

nie wiem czy się nie pomyliłam, ale i tak mniej paskudne te rachunki niż rozwiązywanie układu równań

iteRacj@: jeden z tych punktów należy do prostej x=−1, chyba gdzieś jest pomyłka w rachunkach

Basia: całkiem możliwe; nie liczyłam na kartce, a tu mi się często jakieś liczby poprzestawiają

Basia: współrzędne SA^→ to nie [3k,k] tym razem wektory sobie poprzestawiałam SA^→[x−2;y−4] (x−2)²+(y−4)² = 9 PA^→[x+1;y−13] (x−2)(x−1)+(y−4)(y−13)=0 układ równań chyba podobny do tego który napisał 5−latek

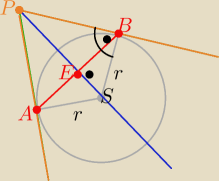
Eta: Witam A może tak: P(−1,13) , S(2,4) r=|BS|= 3 |PS|²=90 to |PB|²=81 ⇒ |PB|=9 Deltoid ASBP ma pole:

	|AB|*|PS|
P= 9*3 i P=		⇒ 54=|AB|*3√10
	2

	9√10
⇒ |AB|=
	5

===================

iteRacj@: Eta podziekuję, owszem, za superszybki sposób rozwiązania ale było całkiem miło wymieniać myśli i sposoby od kilku dni po trochu, a teraz się to skończyło...

Eta: