Zbadaj liczbę rozwiązań równania
Kacper: Mam podane równanie (x3+6x−7)[mx2+(m−3)x+1]=0 i mam zbadać liczbę rozwiązań tego równania ze
względu na wartość parametru m (m ∊ R) oraz napisać wzór i naszkicować wykres funkcji y=g(m),
która każdej wartości parametru m przyporządkowuje liczbę rozwiązań równania.
Z pierwszego nawiasu wyszło mi x=1, a z drugiego przedział m∊(−∞,1)∪(9,+∞),
nie bardzo wiem jak mam dalej to robić.
9 sty 22:52
Qulka: z drugiego to przedział gdy Δ>0 czyli wtedy 2 rozwiązania
9 sty 23:03
PW: A ja nie bardzo wiem, co ma oznaczać "a z drugiego przedział m∊..."
9 sty 23:05
Qulka:
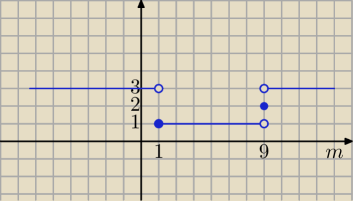
g(m)
9 sty 23:06
Kacper: Czy przypadkiem nie chodzi o to że muszę jeszcze rozpatrzyć Δ<0 i Δ=0?
U siebie w rozwiązaniu widzę jeszcze punkt 0, którego tutaj nie ma na wykresie i jest że
funkcja g(m) ma dwa rozwiązania jeśli m∊{0,9}
9 sty 23:12
PW: Zapomniałeś zauważyć, że funkcja w drugim nawiasie nie musi być funkcja kwadratową (dla m=0
jest liniowa).
9 sty 23:19
Qulka: fakt zapomniałam o m=0 wtedy kropka na 2 i okienko na 3
9 sty 23:20
Kacper: Okej już wszystko mam, dziękuję

9 sty 23:23
Eta:
1/ x3+6x−7=0 ⇒(x−1)(x2−x+7)=0 x=1 −− jedno rozwiązanie
2/ mx2+(m−3)x+1=0
dla m=0 −3x+1=0 −−− jedno rozwiązanie
dla f(1)= m+m−3+1=0 ⇒ m= 1 ⇒ x2−2x+1=0 ⇒ (x−1)2=0 ⇒ x=1 −− jedno rozwiązanie
dla m≠0 i m≠1
mx2+(m−3)x+1=0
Δ >0 .......... 2 rozwiązania dla m∊(−∞,0)U(0,1)U (9,∞)
Δ=0 ....... 1 rozwiązanie dla m=9
Ostatecznie podaj liczbę rozwiązań dla 1/ i 2/
Odp: 1 dla m∊<1,9)
2 dla m∊{0,9}
3 dla m∊(−∞,0)U(0,1)U(9,∞)
i teraz szkicuj wykres g(m)
9 sty 23:26
 g(m)
g(m)
