 Cześć, zadanko z sterometrii:
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości 5 i podstawie
długości 2 \sqrt{5}. Kąt między przekątną ściany bocznej zawierającej podstawę tego trójkąta a
sąsiednią ścianą boczne jest rówy 45 stopni. Oblicz wysokość tego graniastosłupa.
Najpierw wyliczyłem linie przerywana
5+H2=25
h=2√5
Pp=10
10=5h*1/2
h=4
I co teraz brakuje mi choć jednej przekątnej zeby uzyc tw. cos
Cześć, zadanko z sterometrii:
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości 5 i podstawie
długości 2 \sqrt{5}. Kąt między przekątną ściany bocznej zawierającej podstawę tego trójkąta a
sąsiednią ścianą boczne jest rówy 45 stopni. Oblicz wysokość tego graniastosłupa.
Najpierw wyliczyłem linie przerywana
5+H2=25
h=2√5
Pp=10
10=5h*1/2
h=4
I co teraz brakuje mi choć jednej przekątnej zeby uzyc tw. cos jakieś rady?
jakieś rady?  Pozdrawiam
cieplutko <3
Pozdrawiam
cieplutko <3
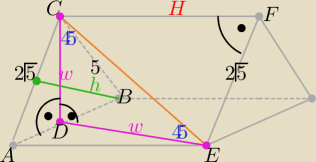
 najpierw liczyłem z wujaszka Pitagora H podstawy
H=2√5
czyli pole podstawy 10
z tego wyliczyłem niebieską linie będącą jedną z wysokości trójkąta − wyszło 4 jak by co
najpierw liczyłem z wujaszka Pitagora H podstawy
H=2√5
czyli pole podstawy 10
z tego wyliczyłem niebieską linie będącą jedną z wysokości trójkąta − wyszło 4 jak by co 
| 1 | ||
P(ABC)=10 i P= | w*5 ⇒ w=4 | |
| 2 |
 No ale na szczęscie
mnie uratowałaś, bardzo doceniam i dziękuję.
A Ciebie PW przepraszam za chaos jaki wytwarzam. Pomyslalem ze jezeli zrobie krotki opis
zadania to kazdy się będzie w stanie domyślić o co mi chodziło. Ale masz rację nastęnym razem
postaram się to solidnej rozpisać.
Pozdrawiam was cieplutko, dziękuje jeszcze raz za pomoc <3
No ale na szczęscie
mnie uratowałaś, bardzo doceniam i dziękuję.
A Ciebie PW przepraszam za chaos jaki wytwarzam. Pomyslalem ze jezeli zrobie krotki opis
zadania to kazdy się będzie w stanie domyślić o co mi chodziło. Ale masz rację nastęnym razem
postaram się to solidnej rozpisać.
Pozdrawiam was cieplutko, dziękuje jeszcze raz za pomoc <3 
