Czy istnieje ścieżka skoczka na szachownicy? Ola: Czy istnieje zamknięta lub otwarta ścieżka skoczka na szachownicy 4x4 i 5x5 dla dowolnych wierzchołków początkowych? Dokopałem się do pracy Schwenka "Which Rectangular Chessboards Have a Knight's Tour?" z 1991r. Udało mi się wywnioskować, że dla 4x4 nie istnieje otwarta ani zamknięta ścieżka skoczka, a dla 5x5 istnieje otwarta, a nie istnieje zamknięta − ale generalnie nie wiem jak to udowodnić. W przypadku 5x5 ścieżki zamkniętej dowód jest prosty. Przekształcamy szachownicę na graf, gdzie wierzchołki to pola, a krawędzie to możliwe ruchy skoczka. Otrzymujemy graf dwudzielny. 5x5=25 więc liczba nieparzysta, a cykl o nieparzystej długości w grafie dwudzielnym nie może istnieć. Co do 4x4 ścieżki zamkniętej, kompletnie nie rozumiem przedstawionego tam dowodu. Oto on: "Załóżmy, że znaleźliśmy cykl. Pokolorujmy wierzchołki w pierwszym i czwartym wierszu na czerwono, a w drugim i trzecim na niebiesko. Takie pokolorowanie nie stanowi już grafu dwudzielnego, ponieważ niektóre niebieskie wierzchołki połączone są z innymi niebieskimi. Aczkolwiek każdy czerwony połączony jest tylko z niebieskimi. W cyklu każdy wierzchołek czerwony musi być rozdzielony niebieskim. Skoro mamy 8 wierzchołków każdego koloru to wierzchołki w cyklu muszą być naprzemiennie. Zaczynając od wierzchołka (1,1) możemy wywnioskować że każdy wierzchołek na nieparzystym miejscu w cyklu jest czerwony. Ale z oryginalnego pokolorowania szachownicy na czarno i biało możemy wywnioskować że każdy wierzchołek na nieparzystym miejscu w cyklu jest biały. Zatem wszystkie czerwone wierzchołki są wierzchołkami białymi, co prowadzi do sprzeczności między wybranymi dwoma sposobami kolorowań. Dochodzimy do wniosku, że cykl nie istnieje." Nie rozumiem wniosków od momentu "Ale z oryginalnego pokolorowania...". Pozostaje jeszcze kwestia ścieżki otwartej 4x4 i 5x5, o której praca niestety nie wspomina. Proszę o pomoc.

kochanus_niepospolitus: Skoczek porusza się dwa ruchy do przodu i jeden w bok −−− o 3 ruchy Skoro porusza się z 1x1 (czyli oryginalnie pola białego) to przemieści się na pole 'czarne', a następnie na 'białe'. Co oznacza, że w nieparzystym miejscu w cyklu będzie znajdował się na polu białym. Z wcześniejszego pokolorowania (na czerowny i niebieski) wniosek był taki, że kolory MUSZĄ być na przemian (bo nie może być dwóch czerwonych kolorów pod rząd − skoczek nie porusza się o 3 miejsca do przodu). W efekcie skoczek poruszający się z punktu (1,1) (kolor czerwony i biały) musi w każdym nieparzystym miejscu cyklu znaleźć się na miejscu 'czerwone i białe' ... a takich miejsc mamy 4, a nie 8. Sprzeczność.

Ola: Super, dziękuję. Żeby udowodnić 4x4 ścieżkę otwarta to będzie tak samo jak wyżej? Zostaje jeszcze 5x5 otwarta :C Masz może jakiś pomysł?

Blee: Jezeli dobrze rozumiem co oznacza droga zamknieta i droga otwarta. To skoro na szachownicy istnieje droga zamknieta (czyli z ostatniego punktu mozna przejsc na punkt poczatkowy) to od razu wiemy ze istnieje droga otwarta. Droge otwarta na szachownicy 4x4 nie mozesz 'obalic' w wczesniej opisany sposob. Jednak tenze opis wskazuje dokladny moment kiedy musialoby dojsc do ruchu skoczka z niebieskiego na niebieski, tak aby czerwone pozycje skoczna byly pozniej na czarnym a nie na bialym (jak dotychczas) polu.

Ola: Zgadzam się, że jeżeli istnieje zamknięta to musi też istnieć otwarta, ale w moim przypadku droga zamknięta nie istnieje 😥

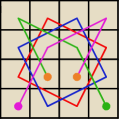
Pytający: Zauważ, że z każdego wierzchołka (rogu szachownicy) masz jedynie dwa ruchy. Zatem żeby się nie zapętlić i odwiedzić przeciwległe rogi, droga musi zaczynać się w którymś z rogów (•). Analogicznie droga musi się kończyć w którymś rogu z drugiej pary przeciwległych rogów (•). Pozostałe 8 nieodwiedzonych pól tworzy dwa rozłączne cykle po 4 pola (−, −). Nie da się bezpośrednio przejść z niebieskiego na czerwony, czyli z jednego pola • trzeba by przejść na −, a drugiego pola • trzeba by przejść na −. Ale pomiędzy −, − nie ma bezpośredniego przejścia, więc taka droga istnieć nie może.

Ola: Dlaczego droga musi sie zaczynać w którymś z rogów? Można znaleźć ścieżkę otwartą w której nie zaczyna się w rogu.

Pytający: Załóżmy, że droga nie zaczyna i nie kończy się w żadnym z rogów. Zatem rogi są gdzieś "po środku" drogi przez wszystkie pola. Z rogów są jedynie 2 możliwe ruchy, a dodatkowo z rogów przeciwległych (tego samego koloru) te 2 możliwe ruchy prowadzą do tych samych 2 pól na środku. Zatem jeśli w żadnym z tych przeciwległych rogów nie mamy początku ani końca drogi, tworzy nam się cykl (zapętlamy się, te pola na środku mają już po 2 dojścia, a więcej nie mogą), więc taka ścieżka nie może istnieć. Stąd wniosek, że przynajmniej 1 z tych rogów jest początkiem/końcem. Ale jako że mamy jeszcze drugą parę rogów naprzeciwległych i sytuacja jest tam analogiczna, wnioskujemy, że w jednej parze musi być początek, a w drugiej koniec.

kochanus_niepospolitus: Olu ... treść zadania ogranicza znalezienie dróg DLA KAŻDEGO z rogów (dowolny wierzchołek)