całki Adrian: Wyznaczyć pole obszaru D ograniczonego krzywymi o równaniach: y=ln(x³), x=1, x=e

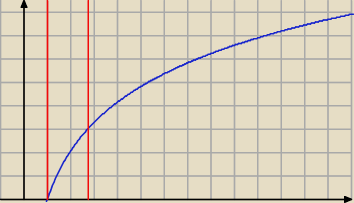
kochanus_niepospolitus: tak trudno narysować 3lnx

kochanus_niepospolitus: dodatkowo zauważając, że 3*lne = 3*1 = 3

Adrian: nie, gdzie tu jest pole ograniczone?

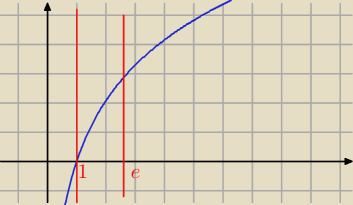
Basia: y=ln(x³) = 3lnx D = ∫₁^e(3lnx)dx J=∫3lnxdx = 3∫lnxdx = 3∫1*lnxdx u = lnx v'=1

	1
u'=		v=x
	x

	1
J=3(x*lnx − ∫x*		dx) = 3(x*lnx − ∫1dx) = 3(x*lnx−x) + C = 3x(ln(x) −1) + C
	x

D = 3e(lne−1) − 3*1(ln1−1) = 3e(1−1) − 3(0−1) = 3

Basia: fakt nie jest ograniczony, a to jest pole tylko tego co jest nad osią OX są trzy możliwości: 1. to co jest między prostymi pod osią OX ma pole nieskończone czyli D→+∞ 2. miała to być prosta y=1 3. zapomniano dopisać "i osią OX"

Adrian: pewnie się profesor pomylił, dzięki