punkty przeciecia Marek: Wyznacz punkty przecięcia xe^1/x z OX. Nie wiem jak to zrobić, bo nie wuiem czy tutaj można dzielić przez x.

Marek: + jak sobie poradzić z asymptotami

Marek: Ktoś by mnie wspomógł?

kochanus_niepospolitus: xe^1/x = 0 ⇔ x=0 lub e^1/x = 0 ... ale wiemy, że e^a ≠ 0 dla dowolnego a, więc jedynym miejscem zerowym jest x=0 ... które jednak wypada, bo nie należy do dziedziny funkcji. Wniosek: brak miejsc zerowych

Marek: Dziekuje. A odnosnie funkcji? Ten x przed e^1/x wszystko mi niszczy.

Marek: Tfu asymptoty*****

Marek:

Marek:

Marek:

Jerzy: Asymptota pionowa prawostronna: x = 0 Asymptota ukośna: y = x + 1

piotr: asymptota obustronna: y = ax + b

	f(x)		f(x)
a = limx→−∞		= limx→−∞e1/x = 1 = limx→+∞
	x		x

b = lim_x→−∞(f(x) − ax) = lim_x→−∞(xe^1/x − ax) = 1

Marek: Jerzy, ale ja wynik mam. Co mi z wyniku jak nie rozumiem... Piotr, a co z x→∞ dla b? Oraz z as. pionowa?

Marek: Bo widze, ze dla a przyrownales lim_x→∞=lim_x→−∞ A w b tego nie zrobiles. Natomiast as. pionowej nie wiem jak poprzekstzalcac to.

Marek:

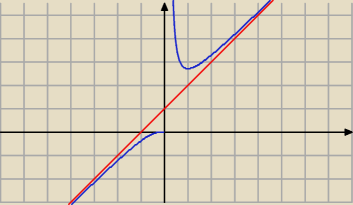
Basia: f(x) = x*e^1/x x∊R\{0}

	e1/x
limx→0+ f(x) = limx→0+
	1   x

	1   − *e1/x   x2
=limx→0+		=
	1   −   x2

lim_x→0⁺e^1/x = +∞ lim_x→0⁻f(x) = 0*0 = 0 prosta x=0 (czyli oś OY) jest asymptotą pionową prawostronną lim_x→+∞f(x) = lim_x→+∞(x*e^1/x) = +∞*e⁰ = +∞ lim_x→−∞f(x) = lim_x→−∞(x*e^1/x = −∞*e⁰ = −∞ nie ma asymptot poziomych więc mogą być ukośne

	x*e1/x
a=limx→+∞		= limx→+∞e1/x = e0 = 1
	x

b = lim_x→+∞[x*e^1/x−x] = lim_x→+∞x(e^1/x−1) =

	e1/x−1		1   − *e1/x   x2
limx→+∞		= limx→+∞		=
	1   x		1   −   x2

lim_x→+∞e^1/x=e⁰=1 masz asymptotę ukośną prawostronną y=x+1

	x*e1/x
a=limx→−∞		= limx→−∞e1/x = e0 = 1
	x

b = lim_x→−∞[x*e^1/x−x] = lim_x→−∞x(e^1/x−1) =

	e1/x−1		1   − *e1/x   x2
limx→−∞		= limx→−∞		=
	1   x		1   −   x2

lim_x→−∞e^1/x=e⁰=1 masz asymptotę ukośną lewostronną y=x+1 czyli y=x+1 jest asymptotą ukośną obustronną

Marek: dziękuje basia!

	1
Pochodna funkcji wyszła mi e1/x(1−		). Jakie są ekstrema tejże funkcji?
	x

Basia: x≠0

	1		x−1
f'(x) = 0 ⇔ 1−		=0 ⇔		=0 ⇔ x−1=0 ⇔ x=1
	x		x

	x−1
e1/x jest stale dodatnie czyli znak pochodnej zależy tylko od znaku wyrażenia =
	x

	x−1
zamiast		możemy zbadać znak wyrażenia x(x−1)
	x

x∊(−∞,0) ⇒ f'(x)>0 ⇒ f↗ x∊(0,1) ⇒ f'(x)<0 ⇒ f↘ x∊(1,+∞) ⇒ f'(x)>0 ⇒ f↗ w p−cie x=0 pochodna wprawdzie zmienia znak, ale funkcja nie jest tam określona więc oczywiście nie ma tu żadnego ekstremum w p−cie x=1 funkcja ma minimum lokalne f(1) = 1*e^1/1 =e

Marek: Zapomniałem podzielić przez e^1/x. Natomiast nie rozumiem skąd wziełaś x(x−1) skoro miejsce zerowe Ci wyszło 1. Wykres wg mnie powinien być liniowy rosnący. Przez co f'(x) ↗ dla x (1,∞) oraz f'(x) ↘ dla x (−∞,0) i (0,1). Mnimum się zgadza.

Jerzy:

	1
Nie widzisz,że znak pochodnej zależy od znaku wyrażenia 1−		,
	x

a wypisujesz swoje niedorzeczne wynurzenia.

Marek: Prawda, ze zależy od tego czyli: 1−1/x=0 i tutaj nie mnożę razy x? Przez co mi właśnie wyjdzie x=1?

Marek: Przecież nawet Basia tak napisała.... Myślałem ze po wyliczeniu miejsca zerowego, można od razu przejść do rysowania wykresu pochodnej

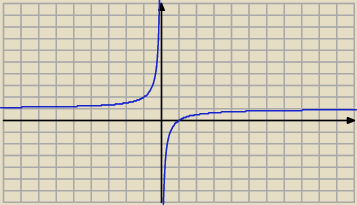
Jerzy: Wystarczy tylko narysować wykres tego fragmentu pochodnej, od którego zależy jej znak,

	1
czyli tutaj: g(x) = 1 −		.
	x

Witać,że w punkcie: x = 1 , pochodna zmienia znak z ujemnego na dodatni, a więc mamy minimum.

Marek: Jerzy, ale nie o to kompletnie chodzi. Ja wiem, że w punkcie x=1 jest minimum. Bo z mojego wykreus to również wynika. Po prostu mamy z Basią inne przedziały, z tego względu, że ona jeszcze ujęła x=0 jako miejsce zerowe, przez co ma parabolę, a ja prostą. Ja zrobiłem wykres funkcji z miejscem zerowym pochodne x=1. I mam takie f'(x) ↗ i f'(x)↘ jak pisałem w poprzednim poście.

Marek:

	1
Ja wziąłem po prostu miejsce zerowe funkcji 1−		, którym jest x=1
	x

Jerzy: Popatrz na wykres 08:58 i ustal jaki ma znak pochodna w przedziałach: (−∞;0) ; (0;1) ; (1:+∞ ) ? I nie wypisuj bzdur,że Basia "ujeła x = 0 jako miejsce zerowe"

Marek: Dobrze widzę... Ale rozumiesz o co mi chodzi czy nie? Widze, że tak jest na wykresie, ale nie rozumiem dlaczego to nie działa tą metodą co zawsze. Czyli Mz pochodnej → oś x, zaznaczamy miejsca zerowe → rysujemy → odczytujemy. Tutaj wyznaczylismy miejsce zerowe x=1 i mimo to wynikiem jest calkiem co innego.

Basia:

	x−1
Basia oczywiście rozważa całą pochodną		, ale w dziedzinie R\{0}
	x

w tej dziedzinie pochodna co do znaku zachowuje się jak funkcja kwadratowa x(x−1), ale w dziedzinie R\{0} jak znam życie i uczniów Marek policzył sobie tak:

	1
1−		<0
	x

	1
1<
	x

x<1 a to nieprawda, bo tutaj przez x mnożyć NIE WOLNO

Marek: Nie policzył sobie tak

	x−1
Nie zrobiłem nawet z tego nierówności. Przyrównałem		po prostu do 0 zeby wyliczyc
	x

miejsce zerowe a nastepnei zrobilem wykres. Gdybym zrobił z tego nierownosc to oczywiscie pomnozyl bym to tzn. x(x−1) ale nigdy tak nie robilem przy maksimum i minimum. Zawsze Mz > wykres > koniec.

Marek: Tak jak etrapez zrobił, tak ja zrobiłem : https://zapodaj.net/cc49a8f799ea0.png.html

Marek: Możecie mi powiedzieć czy dobrze to zrobiłem. Bo tylko prawa strona wykresu mi wychodzi dobrze. Jeżeli chdozi o wklęsłośc wypukłość to wykres 2 pochodnej jest nad osią X, z tego względu ze nie mamy miejsca zerowego. Czyli f(x) U ⇔ x nalezy do R \ {0}

Marek: Tak to u mnie się przedstawia: https://zapodaj.net/a07fb488aacf7.jpg.html Nie zgadza mi sie ten przedział (−∞,0)

Marek: Gdyby druga pochodna bylaby na minusie, to by sie wszystko zgadzalo.

Marek:

Marek:

Jerzy: A do czego Ci potrzebna druga pochodna ?

Marek: Do wklęsłości i wypukłości. Cały przebieg zmienności funkcji.

Marek: Może ktoś pomóc?

Marek:

Marek: Chodzi mi tylko o wylicznie drugiej pochodnej + przedzialy kiedy wypukla kiedy wklesla, a ja juz sobie reszte sam sprawdze. Mam to na jutro

Marek:

Marek:

Marek: