trójkąt mat: W trójkącie ABC z wierzchołka B poprowadzono dwusieczną kąta B która przecięła bok AC w punkcie D tak,że |AD|=|BD| Wiedząc,że |AB|=8 i |BC|=6 Oblicz długość boku AC tego trójkąta

Basia: β=180−3α

6		8
	=
sinα		sin(180−3α)

6*sin(3α) = 8*sinα 3*sin(3α) = 4*sinα 3*sin(α+2α)=4*sinα 3(sinα*cos(2α)+sin(2α)*cosα) = 4sinα 3(sinα*cos(2α) + 2sinα*cos²α) = 4sinα 3sinα(cos(2α)+2cos²α) = 4sinα /:sinα (sinα≠0 bo 0<α<90) 3(2cos²α−1+2cos²α) = 4 12cos²α−3=4

	7
cos2α=
	12

	5
sin2α=1−cos2α=
	12

	7		5		2		1
cos(2α) =		−		=		=
	12		12		12		6

i z tw.cosinusów mamy

	1
AC2 = 82+62 − 2*8*6*		= 64+36−16 = 84
	6

|AC| = √84 = √4*21=2√21

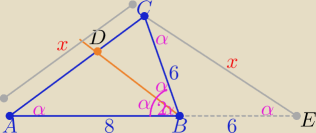
Eta: Trójkąty AEC i BEC są równoramienne i podobne z cechy (kkk)

	|CE|		|BC|
to		=
	|AE|		|CE|

	x		6
		=		i x>0 ⇒ x2=84 ⇒ x=|AC|=2√21
	14		x

=========