Nierówność
Gibon: Rozwiąż nierówność:
(x4−1)(x3+1)(x6−1)(x5+1)≤0
8 sty 00:22
Qulka: xeR\{−1;1}
8 sty 00:27
Gibon: A można z wytłumaczeniem? Bo nie moge sam dojść do wyniku
8 sty 00:28
Qulka: a umiesz rozpisać ze wzorów skróconego mnożenia na kolejne nawiasy?
wyjdzie x=−1 4 razy i x=1 dwa razy i wężyk i się odbijają w obu
8 sty 00:31
Qulka:
(x2−1)(x2+1)(x3+1)(x3−1)(x3+1)(x5+1)
(x−1)(x+1)(x2+1)(x3+1)(x3−1)(x3+1)(x5+1)
1 −1 brak −1 1 −1 −1
8 sty 00:34
Qulka:
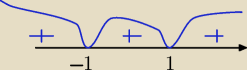
8 sty 00:35
Gibon: (x4−1)=(x2−1)(x2+1)=(x−1)(x+1)(x2+1)
(x6−1)=(x3−1)(x3+1)
Dalej nie wiem co zrobić
jak jest np. (x5+1) to da sie jakoś to rozpisać czy nie?
W ogóle odpowiedź powinna być x∊{−1;1}
8 sty 00:36
mat:
Odp: x∊{−1,1}
8 sty 00:37
Gibon: Dobra już wiem Dzięki serdeczne

8 sty 00:37
Adamm: po prostu
x2k−1 zamień na (x−1)(x+1)
a
x2k+1−1 na x−1
x2k+1+1 na x+1
8 sty 00:38
Qulka: bo ja zamiast mniejsze zauważyłam większe od zera

więc tak tylko −1 i 1

8 sty 00:39
Basia:
miejscami zerowymi są wyłącznie −1 i 1
w przedziale (−∞; −1)
x4−1=(x2−1)(x2+1) > 0
x3+1<0
x6−1 = (x3−1)(x3+1)>0
x5+1<0
(+)*(−)*(+)*(−) = (+)
w przedziale (−1;1)
x4−1 < 0
x3+1>0
x3−1<0
x3+1>0
x5+1>0
też dodatnie
w przedziale (1;+∞)
wszystkie dodatnie
jeżeli się nie pomyliłam to x∊{−1;1}
8 sty 00:41
Basia:
x5+1= (x+1)(x4−x3+x2−x+1)
niezbyt ciekawe i w sumie nic nie daje,chociaż można udowodnić,że x4−x3+x2−x+1 >0 (stale)
8 sty 00:43
Adamm: podstawiasz na coś co ma taki sam znak
czyli nic się nie zmienia
dlatego akurat tak
8 sty 01:18
Basia: gdybyś chciał to bardzo dokładnie rozkładać to tak:
x
4−1=(x
2−1)(x
2+1)=(x−1)(x+1)(x
2+1)
x
3+1=(x+1)(x
2−x+1)
x
6−1=(x
3−1)(x
3+1) = (x−1)(x
2+x+1)(x+1)(x
3−x+1)
x
5+1=(x+1)(x
4−x
3+x
2−x+1)
ponieważ W(x)=x
5+1 ma tylko jeden pierwiastek x=−1
wielomian P(x) = x
4−x
3+x
2−x+1 można rozłożyć tylko na iloczyn dwóch trójmianów kwadratowych
(x
2+ax+b)(x
2+cx+d) = x
4+cx
3+dx
2+ax
3+acx
2+adx+bx
2+bcx+bd=
x
4+(c+a)x
3+(d+ac+b)x
2+(ad+bc)x+bd
stąd
c+a=−1
d+ac+b=1
ad+bc=−1
bd=1
gdyby przyjąć b=d=1 byłoby
a+c=−1
ac = −1
c = −1−a
a(−1−a)=−1
−a
2−a+1=0
a
2+a−1=0
Δ=1+4=5
| | −1 | | −2 | | −2(1−√5) | | 1−√5 | |
wtedy c = |
| = |
| = |
| = |
| |
| | a | | 1+√5 | | 1−5 | | 2 | |
| | 1+√5 | | 1−√5 | |
x4−x3+x2−x+1 = (x2+ |
| x+1)(x2+ |
| x+1) |
| | 2 | | 2 | |
jeżeli to teraz wymnożysz dostaniesz
| | 1+√5 | | 1−√5 | |
(x−1)2(x+1)4(x2+1)(x2−x+1)(x2+x+1)(x2+ |
| x+1)(x2+ |
| x+1) ≤ 0 |
| | 2 | | 2 | |
przy pomocy Δ stwierdzasz, że żaden z trójmianów już nie jest rozkładalny i wszystkie przyjmują
stale wartości dodatnie
a poza tym masz dwumiany w potęgach parzystych
stąd wynika, że to nie może być ujemne czyli nierówność stale się równaniem .....=0
x=−1 lub x=1
8 sty 01:30
Adamm: dokładne rozkładanie jest do dupy
chodzi o to żeby się napracować jak najmniej
a nie żeby robić bezsensowne obliczenia
8 sty 02:48


 więc tak tylko −1 i 1
więc tak tylko −1 i 1 