Geometria analityczna Satan: Punkt B = (−1, 9) należy do okręgu stycznego do osi Ox w punkcie A = (2, 0). Wyznacz równanie tego okręgu. W zasadzie pierwszy raz coś takiego robię o zastanawiam się, czy dobrze kombinuję. Skoro okrąg jest styczny w punkcie A do osi Ox, to środek okręgu leży na prostej x = 2, prawda? Przynajmniej tak myślę, być może błędnie. Jeśli tak jest, jak to udowodnić? Wszystkie wskazówki mile widziane

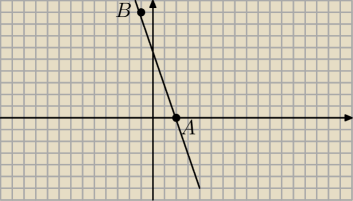
5-latek: wedlug mnie to tak srodek okregu to srodek odcinka AB polowa dlugosci odcinka AB to promien

===: ... cosik Małolat dziś nie w formie

5-latek: Dobry wieczor ===

===: Masz rację Satan ... promień okręgu musi być prostopadły do stycznej w punkcie styczności

===: hej Małolacie

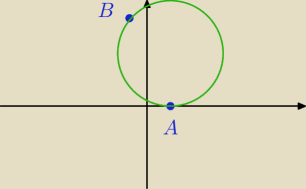
iteRacj@: Dobry wieczór 5−latku środek okręgu nie musi leżeć nalezec do odcinka AB

5-latek: No tak .

5-latek: Dobry wieczor iteRcjo

Eta: 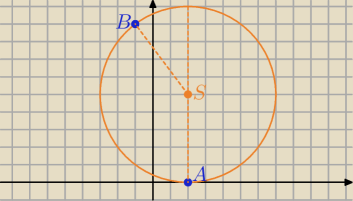Satan dobrze myślisz S(2,y) bo leży na prostej x=2 i |SA|=|SB|=r to |SA|²=|SB|²⇒y²=(2+1)²+(9−y)² ⇒ ..... y=5 ⇒S(2,5) i r=5 o : (x−2)²+(y−5)²=25 ==============

iteRacj@: @Satan środek okręgu jest równoodległy od od obu punktów i należy do prostej, o której piszesz

Satan: Czyli dobrze założyłem. Znaczy, wiem jak pada promień okręgu na styczną, tylko się zastanawiałem, czy to w pełni wystarczy jako dowód No, a teraz wątpliwości zostały w stu procentach rozwiane, dziękuję Wam

Satan: @iteRacja, to wiem, na tej podstawie wyznaczyłem y środka okręgu, potem promień. Tak jak pokazała Eta