Wypuklosc punkty przegiecia asia: Okresl przedziały wypuklosci oraz punkty przecięcia podanych funkcji 1/(1−x²). Wiem, że zależy to od 2 pochodne ale kompletnie nie umiem tego zastosować. Proszę o pomoc z wytłumaczeniem .

Basia: punkty przegięcia to są policz pierwszą pochodną i podaj wynik

===: ... punkty przecięcia powiadasz ...

Kamil: policzy pochodną 2 rzędu i tam gdzie ta pochodna jest dodatnia to funkcja wygląda tak "U" "wypukła" a jak pochodna jest ujemna to funkcja wygląda tak "∩" "wklęsła". miejsca zerowe 2 pochodnej to punkty przegięcia

asia: Przegiecia 😊 pierwsza pochodną to 2x/(x²−1)² a druga − 2 (3x²+1)/(x²−1)³

asia: Wychodzą mi jakieś dziwne rzeczy ze punkty przegiecia to i/pierwiastek z 3 i −i / pierwiastek z 3 . Nie wiem jak tą wypuklosc określić. Jakie to przedziały będą

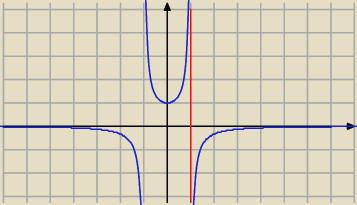
Qulka: brak punktów przegięcia wypukła (−1;1) wklęsła (−∞;−1) oraz (1;∞) malejąca (−∞;−1)u(−1;0) rosnąca (0;1)u(1;∞)

Basia: źle policzyłaś pochodne D = (−∞;−1)∪(−1;1)∪(1;+∞)

	1		2x
f'(x) = −		*(−2x) =
	(1−x2)2		(1−x2)2

	2*(1−x2)2 − 2x)*2(1−x2)*(−2x)
f"(x) =		=
	(1−x2)4

(1−x2)[ 2(1−x2) + 4x2 ]
	=
(1−x2)4

2−2x2+4x2		2+2x2
	=
(1−x2)3		(1−x2)3

f"(x) nie ma miejsc zerowych; punktów przegięcia nie ma x∊(−∞;−1) ⇒ f"(x)<0 ⇒ f jest wklęsła x∊(−1;1) ⇒ f"(x)>0 ⇒ f jest wypukła x∊(1;+∞) ⇒ f"(x)<0 ⇒ f jest wklęsła

Qulka: nie tyle źle policzyła co nie zrozumiała co do niej pisze wolframalpha