as. ukosna Misiek: Wyznaczyć as. ukośną

	x
y=
	lnx

	f(x)
a = lim		wyszło mi 0
	x

x→+/−∞ Pozostaje obliczyć lim(f(x)−ax) x→+/−∞

	x		+∞		+∞
w takim razie lim		= [		]= [		] = ∞
	f(x)		ln∞		∞

x→+∞

	x		−∞
oraz lim		= [		] i tutaj nie wiem bo ln−∞ nie istnieje, wiec wyniku przy
	f(x)		ln−∞

prawostronnej nieskończoności nie ma?

Misiek:

	x
Tam w lim		tym pierwszym zastosowałem regułe de'Hospitala, czy jak to sie tma pisalo
	f(x)

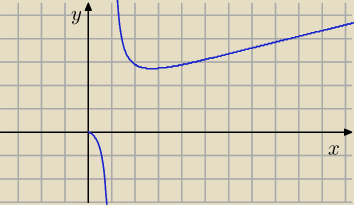
Janek191: Df = (0, + ∞) \ { 1}

Janek191: Asymptota pionowa: x = 1 Brak innych asymptot.

Misiek: Chodzilo o wyzaczenie as. ykosnej a nie narysowanie od razu wykresu

Janek191: a = 0 − brak asymptoty ukośnej

Misiek: Tzn. tak, ale chodzi mi czy dobrze to rozumowałem a nie od razu gotowe rozwiazanie.

Misiek: Ale jeszcze mamy b, jezeli b wyjdzie liczba to mamy as. pozioma, ktora jest specjalna as ukosna jezeli dobrze mowie.

Mila: Misiek, wykres pokazuje , że dla x→−∞ nie liczysz granic, bo dziedzina f(x) to: (0,∞)\{1} x=1 asymptota pionowa

Misiek: Ahhhh.... przeoczyłem. Dziękuję. Mam jeszcze jeden problem. Bo chyba się zgubiłem w liczeniu drugiej pochodnej y, tak żeby mieć dane odnośnie punktów przgięcia, wklęsłości, wypukłości. Ktoś pomoże?

Mila:

	x		ln(x)−1
f'(x)=(		)'=
	lnx		ln2(x)

	1   1   *ln2(x)−(ln(x)−1)*2ln(x)* x   x
f "(x)=		=
	ln4(x)

	1   *[ln2x−2lnx*(lnx−1)] x
=		=
	ln4x

	ln2x−2ln2x+2lnx
=		=
	xln4x

	lnx*(−lnx+2)
=		=
	xln4x

	2−lnx
=
	x*ln3(x)

Misiek: Dziekuje bardzo Mila

Misiek:

	1
Między 3 a 4 linijką jak patrzymy od góry. Gdzie zniknęło
	x

Misiek: Dobra, jestem ślepy Nieważne

Misiek:

	e2
Punkt przegięcia tutaj wychodzi		? Bo etrapez ma samo e2
	2

Mila:

Misiek: Jeszcze jedno ostatnie już pytanie. Miejsce zerowe drugiej pochodnej wychodzi tylko e²?

Mila: f ''(x)=0 2−lnx=0 lnx=2 x=e² 1−lnx>0 1>lnx x<e² druga pochodna zmienia znak przy przejściu przez x₀=e² zatem ma w tym punkcie punkt przegięcia.

Misiek: Pytam, z tego względu ze etrapez ma wykres jako parabole ktora przechodzi przez 1 i e², wg. mnie skoro jest jedno miejsce zerowe powinno przechodzić tylko przez e². Powinna zaczynać się od dołu patrząc z prawej strony z tego względu, że wspolczynnik przy najwyzszej potędze jest ujemny.

Mila: Tylko w e². x=1∉D