 pomoże ktoś?
Naszkicuj wykres funkcji y=g(k) która każdej wartości parametru k (k należy do R)
przyporządkowuje liczbę rozwiązań równania |x2 + 2x − 3| = k|x+3|.
Na razie doszedłem do tego, że k=|x−1| i kompletnie nie wiem co dalej zrobić...
pomoże ktoś?
Naszkicuj wykres funkcji y=g(k) która każdej wartości parametru k (k należy do R)
przyporządkowuje liczbę rozwiązań równania |x2 + 2x − 3| = k|x+3|.
Na razie doszedłem do tego, że k=|x−1| i kompletnie nie wiem co dalej zrobić...
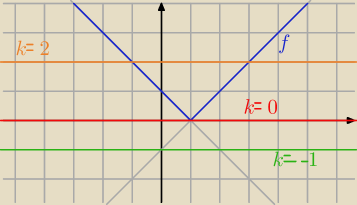 f(x) = I x − 1I
Dokończ
f(x) = I x − 1I
Dokończ 
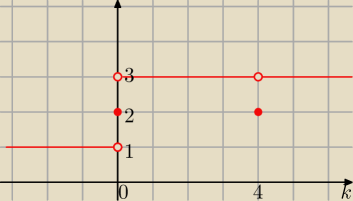
 Ale w odpowiedzi mam taki wykres (nie umiem na tym
narysować XD) y=1 gdy k należy od −nieskończoności do 0 otwarty, y=2 dla k=0 i k=4 oraz y=3
dla k od 0 do nieskończoności za wyjątkiem 4. I skąd im to się wzięło
Ale w odpowiedzi mam taki wykres (nie umiem na tym
narysować XD) y=1 gdy k należy od −nieskończoności do 0 otwarty, y=2 dla k=0 i k=4 oraz y=3
dla k od 0 do nieskończoności za wyjątkiem 4. I skąd im to się wzięło ?
?
 |x2+2x−3|=k|x+3|
y = x2+2x−3
Δ=4−4*1*(−3)=16
√Δ=4
|x2+2x−3|=k|x+3|
y = x2+2x−3
Δ=4−4*1*(−3)=16
√Δ=4
| −2+4 | ||
x1 = | =1 | |
| 2 |
| −2−4 | ||
x2 = | = −3 | |
| 2 |
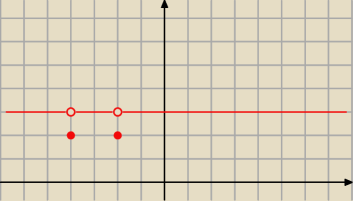
 dla k=0 mamy dwa rozwiązania bo wtedy
|x2+2x−3|=0
x= 1 lub x=−3
dla k<0 mamy tylko jedno rozwiązanie x= −3
bo to równanie postaci:
nieujemna1 = ujemna*nieujemna2
a to jest prawdą ⇔ nieujemna2=0
to co napisałam wyżej ma sens tylko dla k>0
i wtedy będą te trzy rozwiązania
x=−3 x= k+1 x= k−1
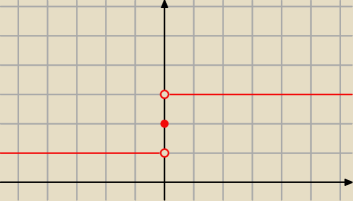
f(k) = 1 k∊(−∞;0)
2 k=0
3 k>0
dla k=0 mamy dwa rozwiązania bo wtedy
|x2+2x−3|=0
x= 1 lub x=−3
dla k<0 mamy tylko jedno rozwiązanie x= −3
bo to równanie postaci:
nieujemna1 = ujemna*nieujemna2
a to jest prawdą ⇔ nieujemna2=0
to co napisałam wyżej ma sens tylko dla k>0
i wtedy będą te trzy rozwiązania
x=−3 x= k+1 x= k−1
f(k) = 1 k∊(−∞;0)
2 k=0
3 k>0

 |x2+2x−3|=|x+3|*|x−1|
to równanie przybiera postać
|x+3|(|x−1|−k)=0 ⇒ |x+3|=0 v |x−1|=k
dla k<0 1 rozwiązanie x= −3
dla k=0 2 rozwiązania x= −3 v x=1
dla k=4 2 rozwiązania x= −3 v |x−1|=4 ⇒ x=5 v x=−3
dla k >0 i k≠4 3 rozwiązania x= −3 v x= k+1 v x= −k+1
{ 1 dla k <0
g(k)= { 2 dla k=0 lub k=4
{ 3 dla k>0 i k≠4
|x2+2x−3|=|x+3|*|x−1|
to równanie przybiera postać
|x+3|(|x−1|−k)=0 ⇒ |x+3|=0 v |x−1|=k
dla k<0 1 rozwiązanie x= −3
dla k=0 2 rozwiązania x= −3 v x=1
dla k=4 2 rozwiązania x= −3 v |x−1|=4 ⇒ x=5 v x=−3
dla k >0 i k≠4 3 rozwiązania x= −3 v x= k+1 v x= −k+1
{ 1 dla k <0
g(k)= { 2 dla k=0 lub k=4
{ 3 dla k>0 i k≠4