Oblicz wartość wyrażenia Szymon: Jaka jest cyfra jednosci wartosci wyrazenia 17 do potęgi 2018 + 13 do potęgi 2018. Uzasadnij odpowiedź.

Qulka: 0

Qulka: bo cyfry jedności przy mnożeniu 17 to 7, 9, 3, 1, 7, 9, 3, 1, 7, 9, 3, 1, 7 czyli co 4 się powtarzają czyli po 2018 będzie 9 bo cyfry jedności przy mnożeniu 13 to 3, 9, 7, 1, 3, 9, 7, 1, 3, 9, 7 czyli co 4 się powtarzają czyli po 2018 będzie 9 po odjęciu jest 0

Szymon: Wielkie dzięki Mam jeszcze jedno pytanie, a mianowicie Oblicz wartość wyrażenia bez używania kalkulatora i mnożenia pisemnego (122018 x 244035 − 122017) : ( 122017 x 244035 + 122018 )

Qulka:

(a+1)(2a+1)−a		a(2a+1)+2a+1−a
	=		=
a(2a+1)+a+1		a(2a+1)+a+1

	a(2a+1)+a+1
=		= 1
	a(2a+1)+a+1

Pytający: Qulka, ale w pierwszym zadaniu jest plus pomiędzy, więc ostatnią cyfrą będzie 8. Swoją drogą wolfram nie zawodzi: https://www.wolframalpha.com/input/?i=last+digit+of+17%5E(2018)%2B13%5E(2018)

Qulka: ewidentnie nie ma znaczenia co jest napisane (powiedziane)... ważne jest co chcemy przeczytać (usłyszeć)

Szymon: Domyśliłem się co do pierwszego zadania, że musiało nastąpić przeoczenie z plusa na minus, dzięki za pomoc. Mam jeszcze trzy zadania, ale to już jutro. Przygotowuję się do testów i Wasza pomoc jest niezastąpiona.

Pytający: Spytałbym o dowód tego twierdzenia... ale to aksjomat.

Pytający: To do Qulki, oczywiście. Szymon, proszę bardzo − namęczyłem się.

Szymon: Proszę o pomoc; zad.3 Środkiem symetrii rombu jest punkt (0,0). Jednym z jego wierzchołków jest punkt (2,−2). Wyznacz współrzędne pozostałych wierzchołków tego rombu, jeśli jego pole wynosi 8. zad. 4 Dane są dwa okręgi współśrodkowe. Cięciwa AB większego okręgu ma długość 40 cm i jest styczna do mniejszego okręgu. Oblicz pole pierścienia kołowego utworzonego przez te okręgi. zad. 5 Stożek przecięto płaszczyzną równoległą do płaszczyzny podstawy i przecinającą wysokość stożka w stosunku 2:3. Oblicz stosunek objętości brył powstałych po rozcięciu. Liczę na Waszą nieocenioną pomoc.

Szymon: Dzięki, że poświęcacie dla mnie swój cenny czas i męczycie się z moimi zadaniami. Takich ludzi ze świecą szukać. Tylko pasjonaci matematyki podejmują wyzwania i pomagają takim jak ja. Wielkie dzięki.

iteRacj@: zad.4 https://brainly.pl/zadanie/1936970 cięciwa ma inna długość, ale idea ta sama i zadanie jasno rozrysowane

iteRacj@: zad.5 https://matematykaszkolna.pl/forum/89085.html tak samo: inne liczby ale idea ta sama zwróć uwagę, czy w Twoim zadaniu przecięcie stożka w proporcji 2:3 liczy się od wierzchołka, czy od podstawy

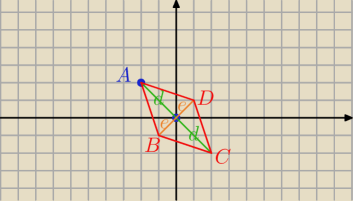
Qulka: d=2√2 więc 2d=4√2 pole =2d•2e/2 =4√2•e=8 więc e= √2 zatem B(−1;−1) C(2;−2) D(1;1)

Szymon: Wielkie dzięki