Zadania z liczb zespolonych
Pomocy: 1.Rozwiąż równanie w zbiorze liczb zespolonych z3=−8(x−iy) x−iy=z sprzężone z kreseczką u
góry.
2.Zaznacz na płaszczyźnie zespolonej liczby zespolone spełniające warunek:
|z2+4|>|z−2i|
3.Niech z0, z1...z4 będą pierwiastkami algebraicznymi stopnia 5 z 32 oblicz ∑od k=0 do
4|2i−zk|2
4.Wiedząc, że z jest liczbą zespoloną o argumencie głównym alfa∊(π/2,π) oraz o module |z|>1
znajdź argument główny liczby zespolonej ([sprzężone(−iz)]z3)/(1−|z|2)
6 sty 21:52
Basia: to pierwsze to ma być układ równań?
6 sty 21:56
Basia:
ad.2
z=x+i*y
z2+4= x2+i*2xy−y2+4 = (x2−y2+4) +2xy*i
|z2+4|= √(x2−y2+4)2+4x2y2
z−2i = x+yi−2i = x+(y−2)i
|z−2i| = √x2+(y−2)2
i trzeba rozwiązać nierówność
6 sty 22:00
PW: Zadanie 1 ma postać
z3 = −8 z̅ ?
Jednym z rozwiązań jest z0=0. Dla pozostałych z po pomnożeniu przez z otrzymujemy
równanie równoważne
z4 = −8 z̅ z
z4 = −8 |z|2.
Dalej można zauważyć, że wobec tego liczba z4 jest liczbą rzeczywistą (bo prawa strona jest
rzeczywista). Myśl dalej, może przedstawić lewą stronę w postaci trygonometrycznej.
6 sty 22:12
Pomocy: Ad 2 jaką nierownosc?
6 sty 22:54
Pytający:
2. Można tak:
|z
2+4|>|z−2i|
|(z−2i)(z+2i)|>|z−2i|
|z−2i|*|z+2i|>|z−2i|
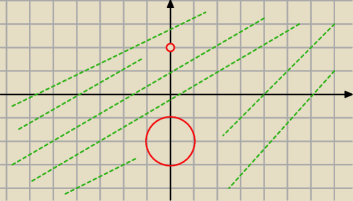
(z=2i ⋀ 0>0) ⋁ (z≠2i ⋀ |z+2i|>1)
Pierwszy przypadek brak rozwiązań (sprzeczność), z drugiego mamy zewnętrze koła o środku −2i
oraz promieniu 1 poza punktem 2i.
6 sty 23:56
 2. Można tak:
|z2+4|>|z−2i|
|(z−2i)(z+2i)|>|z−2i|
|z−2i|*|z+2i|>|z−2i|
(z=2i ⋀ 0>0) ⋁ (z≠2i ⋀ |z+2i|>1)
Pierwszy przypadek brak rozwiązań (sprzeczność), z drugiego mamy zewnętrze koła o środku −2i
oraz promieniu 1 poza punktem 2i.
2. Można tak:
|z2+4|>|z−2i|
|(z−2i)(z+2i)|>|z−2i|
|z−2i|*|z+2i|>|z−2i|
(z=2i ⋀ 0>0) ⋁ (z≠2i ⋀ |z+2i|>1)
Pierwszy przypadek brak rozwiązań (sprzeczność), z drugiego mamy zewnętrze koła o środku −2i
oraz promieniu 1 poza punktem 2i.