geometria analityczna mk: Wyznacz równanie prostej zawierającej dwusieczną kąta utworzonego przez proste k: x+3y−1= 0 m: 6x−2y+1 = 0 do obszaru którego należy punkt P=(3;1) To zadanie już było na forum, ale ciągle nie wiem jak wykazać, w obszarze której prostej znajduje się punkt P, a proste wyszły: 4x−8y+3=0 i 8x+4y−1=0 Wytłumaczyłby ktoś krok po kroku?

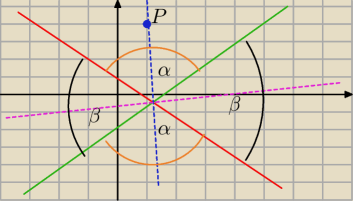
5-latek: Narysuj te proste w ukladzie wspolrzenych i zaznacz zaznacz punkt P=(3,1) Bedziesz wiadomo ktory to obszar Rysunek nie jest do zadania Ma pokazac CI o co biega Dwie przecinajace sie proste tworza dwie pary katow wierzcholkowych (czarne i pomaranczowe Widzisz ze punkt P nalezy do obszaru tam gdzie ten kat α wiec piszsesz rownanie tej dwusiecznej gdzie ten punkt Rownania na dwusieczna sa znane ?

PW:

	1		1
k: y=−		x+		.
	3		3

Dla punktu P=(x_P, y_P)=(3, 1) spełnione są zależności:

	1		1		1		1		2
−		xP+		= −		,3+		= −		< 1=yP.
	3		3		3		3		3

Inaczej mówiąc punkt P ma współrzędną y_P większą niż punkt o tej samej współrzędnej x_P leżący na prostej k, czyli P leży powyżej prostej k. Analogiczne rozumowanie dla punktu P i prostej m pokaże, czy P leży powyżej, czy też poniżej prostej m. W ten sposób określamy, w którym z czterech obszarów leży P.

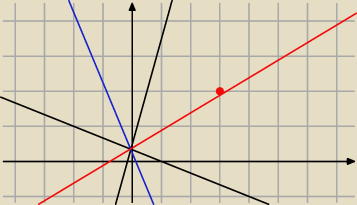
Basia: jak już masz równania dwusiecznych to pomoże rysunek jest to prosta o równaniu 4x−8y+3=0 (wbrew pozorom P do niej NIE należy)

mk: No dobra, już troche zaczynam rozumieć. Tylko co robimy jak już wiadomo gdzie leży P?

mk:

	1
Aaa, czyli dla prostej m: 6x−2y+1=0 −> y=3x+		mamy po podtawieniu punktu P(3,1):
	2

	1		1		2		1
y=9		czyli yp=1<9		, więc yp e (−		;9		)
	2		2		3		2

Czyli mam później podtawić xp do prostych, które mi wyszły po porównaniu k i m czyli: 4x−8y+3=0 i 8x+4y−1=0 i sprwadzić z którego równania wychodzi nam yp, który pasuje do powyższego zbioru?

mk: To by było:

	1		3		1		3		15
dla y=		x+		−> y=		* 3+		−> y=		czyli należy do zbioru yp
	2		8		2		8		8

	1		1		3
dla y=−2x+		−> y=−2*3+		−> y=−5		więc y nie należy do zbioru yp
	4		4		4

	1		3
Czyli szukaną prostą jest y=		x+
	2		8

Dobrze myślę, czy to jakieś kompletne pomieszanie z poplątaniem?

'Leszek: Ogolnie rownanie dwusiecznej kata miedzy prostymi k i m wyznaczamy ze wzoru na odleglosc punktu P(x,y) od tych prostych .

	| x+3y−1|		|6x −2y +1|
W tym przypadku :		=
	√10		√40