zad pytanie: Odcinek o końcach w punktach A= (2, −3) i B = (6, 1) jest podstawą trójkąta równoramiennego, którego jedno z ramion zawiera się w prostej x +2y − 8 = O. Wyznacz trzeci wierzchołek i pole tego trójkąta.

pytanie:

pytanie:

5-latek: zrob rysunek Trojkat rownoramieny to taki trojkat ktory ma ramina rownej dlugosci

Basia: C ∊ symetralnej odc.AB C(x,y) AC = BC AC²=BC² (x−2)²+(y+3)² = (x−6)²+(y−1)² x²−4x+4+y²+6y+9 = x²−12x+36+y²−2y+1 8y = −16x +37−13 8y = −16x+24 y = −2x+3 i układ równań x+2y=9 2x+y=3

pytanie:

pytanie: ten wzor to rownanie okregu ?

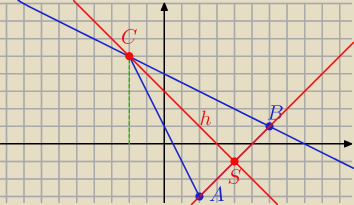
Janek191: S − środek AB S = ( 4, −1) Prosta AB

	4
a =		= 1
	4

y = x + b i S = ( 4, −1) − 1 = 4 + b b = − 5 y = x − 5 ======= Prosta prostopadła: y = − x + k − 1 = − 4 + k k = 3 y = − x + 3 ======== − x + 3 = −0,5 x + 4 0,5 x = − 1 x = − 2 y = 5 C = ( − 2, 5) ========== Pole Δ P = 0,5 I AB I* I SC I =

pytanie: dzięki