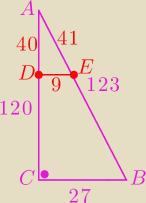
Dany jest trójkąt ABC , w którym o ACB 90 , AB=123 BC= 27 i AC=120 . Na bok kalinka: Dany jest trójkąt ABC , w którym o ACB 90 , AB=123 BC= 27 i AC=120 . Na bok karolina: Dany jest trójkąt ABC , w którym o ACB 90 , AB=123 BC= 27 i AC=120 . Na bokach AC AB i obrano odpowiednio punkty E D i takie, że 40 =AD i 41 =AE . Oblicz pole powierzchni trójkąta AED . Uzasadnij odpowiedz i skorzystaj z tiwerdzenia talesa.

Janek191: P_ΔADE = 0,5*9*40 = 180 j²

PW: kalinko, z twierdzenia Talesa nijak nie da się skorzystać. To popularny błąd, dlatego zwracam uwagę. Twierdzenie Talesa mówi o sytuacji, gdy ramiona kąta zostały przecięte dwiema prostymi równoległymi. (wtedy na ramionach kata wyznaczone są odcinki odpowiednio proporcjonalne). W tym zadaniu nie powiedziano, że prosta DE jest równoległa do prostej CB, a więc nie wiemy, czy jest spełnione założenie twierdzenia Talesa. Janek191 rozwiązał to nie korzystając z tw. Talesa. Czy domyślasz się, jak rozumował?

kalinka: dziękuje

kalinka: chodzi o to że w trojkącie ade rysować należalo wysokość tam tales

PW: Cytat: chodzi o to że w trojkącie ade rysować należalo wysokość tam tales. Nie będę złośliwie komentował. Spróbuj odpowiedzieć na pytanie z 19:56. Jeżeli nie umiesz odpowiedzieć, to cała robota Janka191 na marne.