planimetria AgnieszkaKarolina: Dane są punkty A=(4,2) oraz B=(1,−3). Wyznacz współrzędne punktu C należącego do osi OY tak aby kąt ACB był prosty. matura, listopad 2017 proszę o wskazówki lub rozw. zad

Milo: C leży na OY, więc C = (0,c) dla pewnego c∊ℛ AC^→ = [−4, c−2] BC^→ = [−1, c+3] wektory są prostopadłe ⇔ ich iloczyn skalarny jest zerem (−4)*(−1) + (c−2)(c+3) = 0 4 + c² + c − 6 = 0 c² + c − 2 = 0

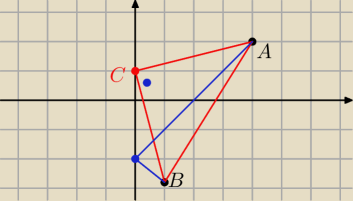
Basia: są różne sposoby; na przykład tak C(0;y) AC^→=[0−4;y−2] = [−4;y−2] BC^→=[0−1;y−(−3)] = [−1;y+3] AC^→⊥BC^→ ⇔ AC^→◯BC^→=0 stąd (−4)*(−1) + (y−2)(y+3) = 0 4+y²+3y−2y−6=0 y²+y−2=0 Δ=1−4*1*(−2)=9 √Δ=3

	−1−3
y1=		= −2
	2

	−1+3
y2=		= 1
	2

C(0;−2) lub C(0;1) można też zwyczajnie z długości i twierdzenia odwrotnego do tw.Pitagorasa

jc: Jeszcze inne rozwiązanie. Przecięcie okręgu o środku (1/2)(A+B) i promieniu (A−B)²/4 z prostą x=0. (x−5/2)² + (y+1/2)²=34/4, x=0 (5/2)² + (y+1/2)²=34/4 (y+1/2)²=9/4 y=−1/2±3/2=1, −2

AgnieszkaKarolina: Dziękuję Wam bardzo