stereometria
AgnieszkaKarolina: Dany jest graniastosłup prawidłowy trójkątny o dolnej podstawie ABC
i górnej A'B'C'. Przekątna ściany bocznej tworzy z krawędzią
podstawy kąt 60 stopni. Pole ściany bocznej graniastosłupa
jest równe 2
√3. oblicz pole trójkąta ABC'.
Zadanie z matury, listopad 2017
proszę o pomoc
6 sty 10:05
Basia:
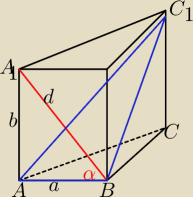
trójkąty ABC i A'B'C' oczywiscie są równoboczne
i wszystkie ściany boczne są przystające
a
√3=b
a*b = 2
√3
a
2√3 = 2
√3
a
2=2
a=
√2
b =
√2*
√3 =
√6
d
2 = a
2+b
2 = a
2+3b
2=4b
2
d = 2b = 2
√6
trójkąt ABC
1 to trójkąt równoramienny
podstawa = a =
√2
ramiona = d = 2
√6
| | √2 | | 2 | | 1 | | 49 | |
h2 = ( |
| )2+(2√6)2 = |
| +4*6 = 24+ |
| = |
| |
| | 2 | | 4 | | 2 | | 2 | |
| | 1 | | 7 | | 7 | |
PABC1 = |
| *√2* |
| = |
| |
| | 2 | | √2 | | 2 | |
6 sty 10:34
Qulka:
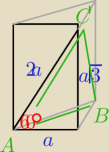
a•a
√3=2
√3 więc a=
√2
zielony
h
2=(2a)
2−(a/2)
2
Pole a•h/2
6 sty 10:39
AgnieszkaKarolina: Skąd mamy d2=a2+b2=a2+3b2=4b2
6 sty 14:22
Basia: z tw.Pitagorasa i z tego, że b=a√3
6 sty 14:24
AgnieszkaKarolina: d2=a2+b2=a2+3a2=4a2
6 sty 14:27
Basia: rzeczywiście pomyliłam się; wzięłam a=b√3 a to nieprawda
wszystko dalej też trzeba poprawić
6 sty 14:28