planimetria AgnieszkaKarolina: wyznacz długość boku kwadratu wpisanego w trójkąt równoboczny o boku a w ten sposób, że jeden bok kwadratu jest zawarty w boku trójkąta, a dwa wierzchołki kwadratu należą do pozostałych boków trójkąta. Zadanie − próbna matura z zmatematyki listopad 2017 za wszelkie wskazówki lub rozw. wielkie dzięki

zagajnik: mam prośbe podasz stronę z arkuszem z tej probnej matury listopad 2017 ?

wmboczek: dzielisz trójkąt wysokością i układasz proporcję z podobieństwa trójkątów

Qulka: http://arkusze.gieldamaturalna.pl/

zagajnik: czy to jest a=3+2√3 ?

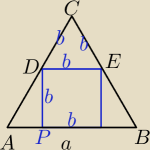
Basia: dane: a b − długość boku kwadratu 0<b<a trójkąty ABC i DEC są podobne czyli DE=DC=EC=b stąd |AD|=a−b

	PD		b
sin60 −		=
	AD		a−b

b		√3
	=
a−b		2

2b = (a−b)*√3 2b = a√3−b√3 2b+b√3 = a√3 b(2+√3) = a√3

	a√3		a√3(2−√3)
b =		=		= a(2√3−3)
	2+√3		4−3

Basia: tam oczywiście ma być sin60= a nie sin60−

AgnieszkaKarolina: wielkie dzięki

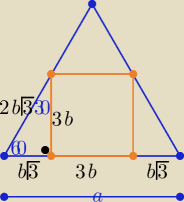
Eta: Można też tak : z własności trójkąta "ekierki" o kątach 60^o,30^o,90^o 3b −−− dł boku kwadratu i a=2b√3+3b −−− dł. boku trójkąta a=b(2√3+3) /*(2√3−3) ⇒ a(2√3−3)= b(12−9) 3b=a(2√3−3) ===========

AgnieszkaKarolina: dziękuję