| 6x2 + x − 1 | ||
f(x) = | ||
| 2x2 +7x −4 |
| 1 | ||
D = r − {−4, | } | |
| 2 |
| 6x2 + x − 1 | ||
f(x)= | ||
| 2x2 +7x −4 |
| 1 | ||
D=R−{−4, | } | |
| 2 |
| 6x2 + x − 1 | 91 | |||
limx→(−4)− | = [ | ] = +∞ | ||
| 2x2 +7x −4 | 0+ |
| 6x2 + x − 1 | 91 | |||
limx→(−4)+ | = [ | ] = −∞ | ||
| 2x2 +7x −4 | 0− |
| 1 | ||
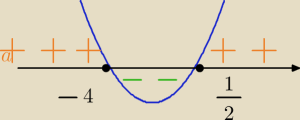
sprawdzamy istnienie asymptoty pionowej dla x= | , liczymy granice lewo− i prawostronną | |
| 2 |
| 6x2 + x − 1 | 1 | |||
limx→(12)− | = [ | ] = −∞ | ||
| 2x2 +7x −4 | 0− |
| 6x2 + x − 1 | 1 | |||
limx→(12)+ | = [ | ] = +∞ | ||
| 2x2 +7x −4 | 0+ |
| 1 | ||
prosta x= | jest asymptotą pionową obustronną | |
| 2 |