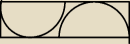
Geometria abcdef: Wiemy że szerokość prostokąta wynosi 30. Półkola są takie same. Obliczyć powierzchnię poza tymi półkolami w prostokącie

abcdef: ?

Maatema: Szerokość to który bok prostokąta ? "Podstawa" ?

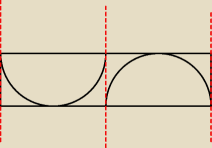
Pytający: Te półkola się stykają czy jak u mnie na rysunku?

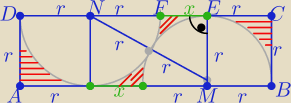
Eta: |AB|=|DC|=3r+x P(ABCD)=r(3r+x)= 3r²+rx P( części zakreskowanych) = P(ABCD) − P(całaego koła −− cztery ćwiartki) P= 3r²+rx−πr² Należy wyznaczyć długość "x">0 Z tw. Pitagorasa w ΔMNE: r²+(r+x)²= 4r² ⇒ x²+2rx −2r²=0 Δ = 12r² , √Δ=2r√3 to x= −r+r√3 = r(√3−1) >0 zatem P= 3r²+r²(√3−1)−πr² = r²(2+√3−π) dla r=30 P= 900(2+√3−π) ==============