geometria AgnieszkaKarolina: Punkt D jest środkiem okręgu wpisanego w trójkąt ABC, a punkt E jest spodkiem dwusiecznej poprowadzonej z wierzchołka A. Znajdź nie rysując dwusiecznych środek okręgu dopisanego do boku naprzeciw wierzchołka A. Ma ktoś jakiś pomysł

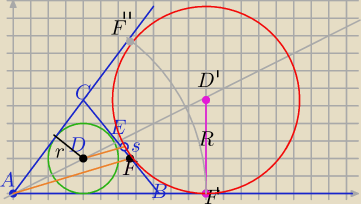
Mila: 1) Środek okręgu dopisanego do BC leży na dwusiecznej kąta A 2) Szukamy punktu styczności okręgu dopisanego z bokiem BC 3) Znajdujemy środek BC ( trochę tu trudno, na kartce łatwo)− punkt S 4)Rysujemy odcinek DS, rysujemy z punktu A równoległą do DS⇒F 5) AF|| DS, Punkt F jest szukanym punktem styczności 6) |BF|=|BF'| − punkty styczności sa jednakowo odległe od wierzchołka B 7) wystawiamy prostopadłą do AB w p. F'⇒punkt przecięcia z dwusieczną − punkt D' 8) D' −środek szukanego okręgu R=|D'F'|− promień szukanego okręgu Oczywiście pamiętaj, że to ma być konstrukcja− tylko cyrkiel i linijka

AgnieszkaKarolina: Bardzo Ci dziękuję

Mila: No to Twoja Pani zaszalała z tymi zadaniami

AgnieszkaKarolina: Troszkę

AgnieszkaKarolina: A może ktoś miałby pomysł jak to samo zadanie zrobić w ten sposób żeby użyć tylko i wyłącznie linijki

AgnieszkaKarolina: Ludziska macie pomysł jak okrąg dopisany skonstruować tylko za pomocą linijki

Mila: Żarty sobie stroisz? Kto rysuje okrąg za pomocą linijki? Podałam proste rozwiązanie, a Ty szukasz nie wiadomo czego.

Mila: Raczej powinnaś zapytać o co innego, ale sądzę, że nie chciało Ci się przeczytać, ze zrozumieniem tego co napisałam.

AgnieszkaKarolina: Może doprecyzuje: mam znaleźć środek okręgu dopisanego do boku tylko za pomocą linijki