geometria trójkąta AgnieszkaKarolina: Dane są trzy różne rozłączne zewnętrznie okręgi O₁ O₂ oraz O₃ o środkach odpowiednio P₁ P₂ oraz P₃. Te dwie styczne, które rozdzielają okręgi O₁ i O₂ przecinają się w punkcie A₃. Analogicznie definiujemy A₁ oraz A₂. Wykaż że punkty A₁ A₂ oraz A₃ leżą na jednej prostej. Jeśli ktoś byłby w stanie pomóc to bardzo proszę

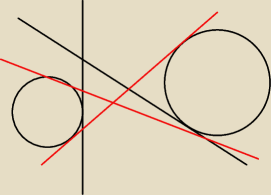
Basia: co to znaczy, że styczne rozdzielają okręgi? bo takich par jak te czarne jest nieskończenie wiele chodzi o takie jak te czerwone?

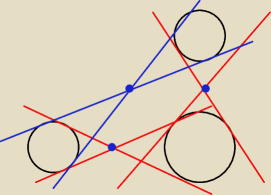
Basia: zdecydowanie nie leżą na jednej prostej czyli to też nie to chyba czegoś w tej treści brakuje

Basia: może środki tych okręgów są współliniowe, no ale wtedy to oczywiste

ale jak to?: Tutaj jest podobne zadanie, tylko inne pytanie zadane przez autorkę. https://matematykaszkolna.pl/forum/365704.html Nie wiem, czy są to podobne zadanie czy to to samo zadanie, tylko coś źle przepisana końcówka. Poprzednie zadanie jest rozwiązane na stronie: http://www.deltami.edu.pl/temat/matematyka/geometria/planimetria/2011/02/01/Twierdzenie_Cevy/ Autorka musi się określić co do tego "małego zamieszania".

AgnieszkaKarolina: To są dwa różne zadania. Treści zadań są prawidłowo spisane.

ale jak to?: AgnieszkaKarolina, jeśli mogę spytać to skąd masz te zadania. Jest to jakaś książka, zbiór zadań czy coś innego. Pytam dlatego, gdyż te zadania bardziej bliżej treścią odpowiadają na olimpiady, niż zadania maturalne.

AgnieszkaKarolina: Dostaliśmy kartkę z zadaniami na dodatkowych zajęciach.

Basia: Jeżeli treść przepisałaś poprawnie to na rysunku widać, że teza postawiona w zadaniu jest fałszywa. I koniec.Jeden kontrprzykład obala twierdzenie.