pochodna janusz: cześć czy pochodna f(x)=|sinx| to |cosx|?

Benny: Nie

janusz: więc może pokazałbyś jak to wyliczyć?

Benny: Rozpisz sobie f(x) na przedziały i wtedy licz.

janusz: ćw 1. sinx pochodna cosx ćw 2. sinx pochodna cosx ćw 3. −sinx pochodna −cosx ćw 4. −sinx pochodna −cosx tak? bo nie wiem dokładnie o co chodzi

Jerzy: Wskazówka: |sinx| = √sin²x

Jerzy: Potem ustal, gdzie ta pochodna istnieje.

janusz:

	1		1
pochodna f(x)=√sin2x=		*(sin2x)'=		*2(sinx)*(sinx)'=
	2√sin2x		2√sin2x

1		sinx*cos
	*2(sinx)*cosx=
2√sin2x		√sin2x

dobrze?

Jerzy: Tak, ale nie skracaj przez 2.

	2sinxcosx		sin2x
f'(x) =		=
	2√sin2x		2√sin2x

janusz: z tym ustalaniem gdzie istnieje to nie bardzo mogę sobie poradzić. napewno pochodna nie istnieje w x=0 bo mianownik nie może być zerem

Jerzy: A czy mianownik zeruje sie tylko dla: x = 0 ?

janusz: dla wszystkich argumentów dla których funkcja sin²x ma wartości 0 pochodna nie istnieje, czyli dla x=0+kπ gdzie k∊Z

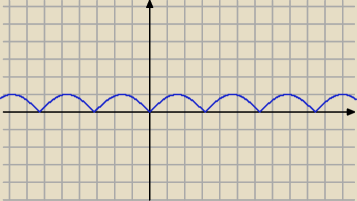
Jerzy: Tak. Widać to wyraźnie na wykresie funkcji: f(x) = |sinx| ( tam , dzię są "szpice" )

janusz: wielkie dzięki