Przekształcenie wykresu funkcji tryg. kasia123: Dzień dobry, bardzo proszę o pomoc. Mam narysować wykres funkcji i nie jestem pewna czy dobrze myślę. y = − cos (1/2x − pi/4) = − cos [1/2 (x − pi/2)] kolejność w jakiej robię: 1) rysuję −cos x 2) rozszerzam (nie wiem jak na to się mówi dokładnie, robię górki i dołki 2 razy większe) 3) przesuwam o wektor [0,pi/2] Czy dobrze myślę? I czy punkt 1) i 2) można ze sobą zamienić?

Jerzy:

	x		π
y = −cos(		−		)
	2		4

1) cosx

	x
2) cos(		) (rozciągnięcie)
	2

	x		π
3) cos(		−		) (przesunięcie w prawo)
	2		4

4) odbicie względem osi OX

cotyniepowiesz98: Chyba doprowadzi to do takiego samego wykresu... prawda?

Jerzy:

	x		π		π   x −   2
Wykres bedzie ten sam , bo: − cos(		−		) = − cos(		)
	2		4		2

kasia123: A więc mój sposób również jest dobry, tak? Czy to jest jakiś przypadek, że po prostu fartem wyszło tak samo?

kasia123: i proszę o odpowiedź czy punkt 1 i 2 w mojej wypowiedzi, można zamienić kolejnością

Jerzy: Doprecyzuj pkt 2)

kasia123: A więc wtedy rysowałabym tak: 1) cos 1/2x 2) −cos1/2 (odbijam wzg osi X) 3) przesuwam o wektor [0,pi/2]

Jerzy: Co to znaczy: "górki i dołki 2 razy wieksze" ?

kasia123: I jeszcze jedno pytanie, w sumie dość podobne. Załóżmy, że mam funkcję 4 cos 1/2x to mogę zrobić to tak: 1) 4cosx 2) rozszerzam lub 1) cos1/2x 4) wartości mnożę przez 4 obie drogi są dobre, zgadza się?

kasia123: Haha Kurcze nie wiem, jak to ładnie wytłumaczyć, Jerzy Chodzi mi o to, że jak np. był punkt (pi/2,0) to znajdzie się on w miejscu (pi,0)

Jerzy: Nie. 4cosx ≠ 4cos(x/2)

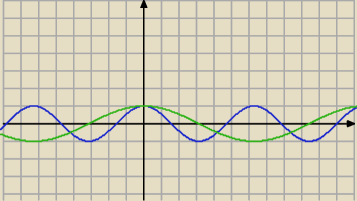
Jerzy: Niebieski: cosx Zielony: cos(x/2)

kasia123: Ale ja nie napisałam, że 4cosx ≠ 4cos(x/2).

kasia123: Jerzy, ja umiem te wykresy. Chodzi mi wyłącznie o kolejność przekształcania.

kasia123: Narysowałam te 4cos1/2x na dwa sposoby, które napisałam Ci wyżej i wyszly tak samo

Jerzy: Tak, wyjdzie to samo.

kasia123: Dziękuję Ci bardzo za pomoc i rozwianie moich wątpliwości. Miłego dnia.