najwieszke i najmniejsze wartości wojtek: znaleźć największe i najmniejsze wartości funkcji f(x) = 1−|9−x²| na <−5,1> g(x) = √3+2x−x² w tym pierwszym jak obliczam, to mi wychodzi x=3 v x=−3 (to nie jest w zakresie) to licze tylko f(3) =1 f(−5)=−15 f(1)=−7 to tyle?

	1
a w drugim zakres po obliczeniu wychodzi <−1;		}
	3

i od f(−1),f(1/3) wychodzi 0 jak to zrobić?

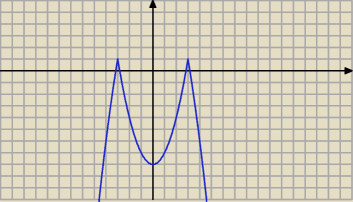
Jerzy: To wykres f(x)

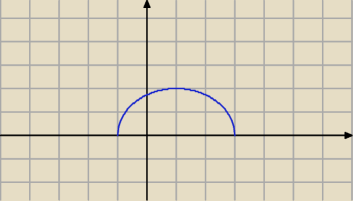
Jerzy: To wykres g(x)

wojtek: dlaczego wykres fx nie jest odwrotnie

Jerzy: f(x) = − [ |9 − x²| −1 ] , a to co jest w nawiasie kwadratowym to: |9 − x²| przesunięte o 1 w dół.

Basia: ad.1 w przedziale <−3;1> 9−x²≥0 i masz f(x) = 1−9+x² = x²−8 ta funkcja najmniejszą wartość osiąga dla x=0 i jest to f(0)=−8 f(−3) = 9−8=1 f(1) = 1−8 = −7 w przedziale <−5;−3) 9−x²<0 i masz f(x) = 1−(−9+x²) = −x²+10 ta funkcja wartość największą osiaga dla x=0∉<−5;−3) f(−5) = −25+10 = −15 czyli najmniejszą wartością f(x) jest f(−5) = −15, największą f(−3)=1

Jerzy: W drugim minima są oczywiste, natomiast maksimum jest tam, gdzie trójmian osiaga wartość maksymalnę, czyli f(1) = 2