Znaleźć przedziały monotoniczności oraz ekstrema lokalne funkcji: Mati: Proszę o sprawdzenie Znaleźć przedziały monotoniczności oraz ekstrema lokalne funkcji: f(x) = √3x−x³ wyszło mi że funkcja jest rosnąca w przedziałach (−1, 0); (0, 1) malejąca w przedziałach (−∞, −√3); (−√3, −1); (1, √3), (√3, ∞) i maximum w punkcie (1, √2), minimum − brak

Jerzy: Trzy minima: (−√3;0) (0,0) (√3;0) Jedno maximum: (1;√2) Maleje: (−∞;−√3) U (1;√3) Roznie: (0 ; 1)

Jerzy: Zacznij od dziedziny tej funkcji, bo najwyraźniej jej nie wyznaczyłeś/a

Mati: Faktycznie, nie uwzględniłem dziedziny funkcji, teraz przedziały monotoniczności wyszły mi dobrze, ale nie wiem skąd się wzięły minima

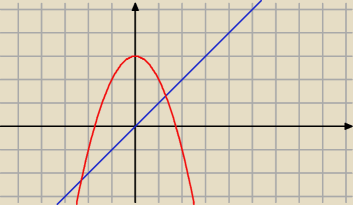
Basia: rysunek jest do określenia dziedziny 3x−x³≥0 x(3−x²)≥0 x∊(−∞;−√3>∪<0;√3> lim_x→−∞f(x) = lim_x→−∞ √x³(3/x² − 1)= −∞(0−1) = +∞ f(−√3) = −3√3+3√3=0 f(0)=0 f(√3 = 3√3−3√3 = 0

	1		3(1−x2)
f'(x) =		*(3−3x2) =
	2√3x−x3		2√3x−x3

f'(x)=0 ⇔ 1−x²=0 ⇔ x = ±1

	3
znak pochodnej zależy tylko od znaku y=1−x2 bo		jest stale dodatni
	2√3x−x3

x∊(−∞;−√3) ⇒ f'(x)<0 to funkcja maleje (od +∞ do 0) x∊(0;1) ⇒ f'(x)>0 ⇒ f rosnie (od 0 do f(1)=√3−1=√2) x∊(1;√3) ⇒ f'(x)<0 ⇒ f maleje (od √2 do 0) wykres i komentarz w kolejnym poście

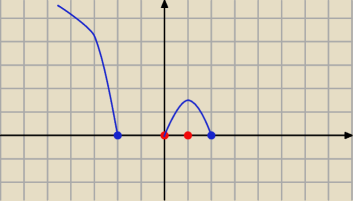
Basia: kropki niebieskie to −√3 i √3 dla x=1 oczywiście mamy maksimum lokalne natomiast minima, które mamy dla x= −√3, x=0 i x=√3 nie wyjdą z rachunku pochodnych z tej prostej przyczyny, ze funkcja jest w tych punktach nieróżniczklowalna tak często jest na końcach przedziałów tworzących dziedzinę

Mati: ok, dziękuję za wytłumaczenie